进阶延迟处理 · 环境

雾

上一节我们成功为场景添加了还算能看的光照，但仍有一个不可忽视的问题：场景没有纵深感。在现实生活中，由于大气的存在，从远处物体进入我们眼中的光线会被空气中的小分子散射，最终看起来就像消隐进天空了一样，这些散射粒子就是所谓的雾气。雾气浓度与场景纵深挂钩，还可以在一定程度上用来遮瑕，并且单纯地绘制雾气的成本相对较低。

简单水平雾

雾气有很多处理方法，让我们从最简单的深度雾开始。和之前一样，说到位置信息，我们就离不开深度图。还记得我们第一章第一节中第一次体验延迟处理效果时吗？当时我们构建了一个获取线性深度图的函数 float LinearizeDepth(float depth) 用来处理那个奇怪的饱和度淡入特效，原来你一直与我同在。它可以返回场景的视口空间 Z 值：

uniform float near;
uniform float far;

float LinearizeDepth(float depth) {
    float z = depth * 2.0 - 1.0;
    return (2.0 * far * near) / (far + near - z * (far - near));
}

和之前的思路一样，我们需要将线性深度除以 far 来获取归一化线性深度：

float depth_linear = LinearizeDepth(depth);
float depth_normalized = depth_linear / far;

这一次，我们依旧用 mix() 函数来进行处理，只不过我们这一次要混合的不再是饱和度，而是雾色。和天空颜色一样，OptiFine 也为我们提供了当前群系的雾色 fogColor：

uniform vec3 fogColor;
[... main ...]
vec3 fogColorG = vpow(fogColorG, GAMMA); // 记得转到线性空间！
fragColor.rgb = mix(fragColor, fogColorG, pow(depth_normalized, 2));

你应该已经注意到了，我们使用线性深度的平方，这样可以让雾气在近处衰减得更快，以免让整个场景都雾蒙蒙的。现在我们已经可以看出很明显的场景纵深了：

当然，你也能明显看出，这种雾气受镜头朝向影响，雾气边缘看起来就像是一个随着镜头运动的平面，Minecraft 早期的流畅迷雾就是如此处理的。一个更好的衰减方案，是使用场景相去视角的水平距离，而不是单纯的 Z 轴：

float fogDensity = pow(min(length(worldPos.xz), 1.0), 2);
fragColor.rgb = mix(fragColor, fogColorG, fogDensity);

一定要记得钳制距离的最大值，因为归一化坐标围成的形状是矩形，对边距离最大可能会达到，导致混合出错。

虽然我们的场景已经初具纵深，但你很快就会发现天空也因为其处于最大深度而一并被雾气遮蔽，虽然我们可以直接使用天空判定来禁用雾气，但这会导致很难看的断层，就像原版那样。

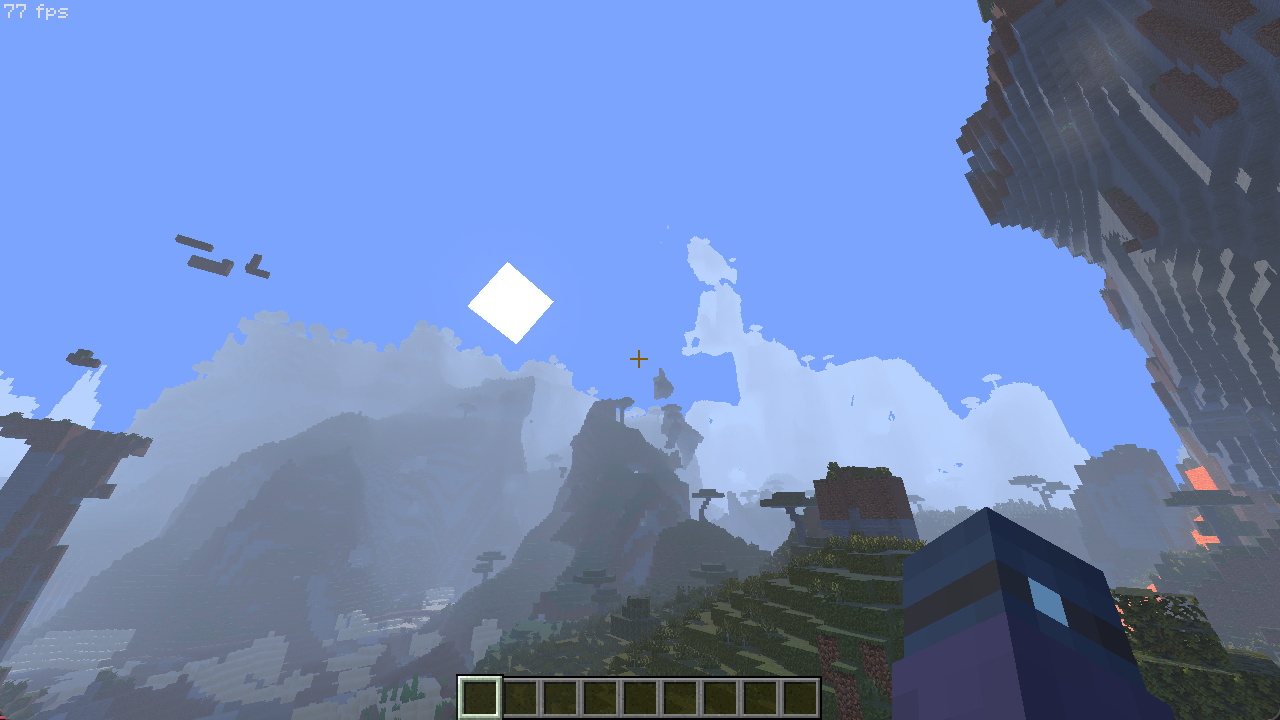
我们希望找到一种可以同时遮蔽环境和天空，还不会断层的雾气，这就是我们的下一步计划。

衰减

在现实中，受重力的影响，散射粒子不会在大气中均匀分布，倾向于散射环境光的大质量粒子总体分布在比较低的海拔上，而倾向于散射日光形成蓝色天空的细小分子则分布得更广。最终地平线附近被雾气遮蔽，而天空却依然清晰可见。

因此，除了水平上的衰减外，我们的雾气也还应该在竖直方向上进行衰减。之前的雾气我们都在视口空间完成，这和雾气越远越浓天然契合，然而在竖直方向上，固定海拔的雾气基本浓度不会随着视角变动而改变，因此我们需要使用绝对世界空间的轴坐标。

Minecraft 的普通世界海拔默认为 63，因此我们可以将海平面的雾气浓度设置为 1，往下不再增加，往上逐渐衰减，直到世界的建筑高度 320 层衰减至 0。当然，这些衰减方式也全凭你自己的喜好。

float altitude = worldPos.y + cameraPosition.y;
fogDensity *= pow(remapSaturate(320.0, 63.0, altitude), 2);

这样，我们就完成了基本的高度雾：

当然，目前的雾气缺陷仍然很明显，如果我们抬头观察同一竖直线上的表面，由于高空中竖直方向上雾气浓度已趋于 0，简单地将高度雾浓度与水平雾浓度相乘会导致远处的物体变得更加清晰，而近处的物体反而被笼罩在雾中。直觉上来说，高处的物体应该消隐得更慢，但不可能比同一条线上其他近处的物体更加清晰。

出现的问题也很正常，因为我们在水平方向上通过俺寻思考虑到了雾气随距离远去的累积效应，但在竖直方向上却直接取用了片元处的雾气浓度乘数，换句话说，没有完全考虑从视口到片元的视线上累积的雾气。当我们斜向上看向远处时，片元的距离与雾气累积浓度的关系看起来就像这样：

另一个问题是，简单的幂和线性衰减过于生硬。描述大气衰减的压高公式指出，地球的大气是随海拔上升呈指数衰减的，而可见性与雾气浓度也不是简单的线性关系。因此，我们需要一个能更完美地描述雾气浓度的公式。

指数衰减积分雾

如果我们视同一海拔上的大气浓度为均匀，那么雾气浓度就可以改写为：

其中表示高度，表示雾气基础密度，表示随高度的衰减速率。

在视线方向上的雾气总浓度为：

其中积分区域为摄像机与目标点的连线，表示线上的距离，和分别是两点的相对坐标差值，和表示摄像机与目标点的世界空间高度，。该式也可以扩展到三维空间中，只需要将项更改为。这个公式是方向无关的，因此积分式和坐标差还要取绝对值。

实际应用时，这个算式可能会在视线水平时出现除 0 错误，尽管我们可以用瞪眼法看出，但 GPU 不会自主处理这种极限情况。因此我们可以手动判定，在极限情况下替换为原函数：

如 果 其 他

当然，考虑到浮点和除法精度，不能严格等于 0，可以取作为极限逼近。

最后的最后，求场景的可见性就比较简单了，它与雾气浓度相关的函数可以写成，其中是与雾气和距离的相关系数，也就是我们之前求到的。

好了，烦人的原理部分到此为止，我们来开始翻译 GLSL 吧。为了便于随时确认，我们将公式誊写下来：

如 果 其 他

这里我们取极限逼近函数使用了片元的高度而不是视口高度，理论上来说，这两个高差其实无所谓，只是在极端情况下能随片元的细微高差而变化。

我们先来处理公式中的那些常量和可调宏，包括自然常数、基础浓度和衰减速率。基础浓度和衰减速率我们将来都会加入设置中，因此我们用宏定义它们：

#define FOG_BASE_DENSITY 0.1
#define FOG_HEIGHT_FALLOFF 0.02
#define FOG_START_HEIGHT -120

我们会在线路上进行积分，每个微元的浓度就不必太高了，衰减系数在双重指数（）上，我们应当在千分位上微调。此外，我们还添加了一个 FOG_START_HEIGHT 用于偏移函数零点，它会被加到和上，在这个高度以下的海拔浓度倍率会超过 1 并指数增长。

由于自然常数全部都用于指数函数，GLSL 为我们提供了内建的 exp(float x) 来计算，所以我们不需要再单独声明它。

接着再来看里面的变量，说来也不多，只有片元距离、高差和视口与片元的海拔。

高差和片元距离都是相对数据，因此我们可以直接在相对世界空间求解它们。非常简单，就是片元坐标的分量取绝对值，距离则是片元的模长。注意到距离总是和浓度一起出现，我们可以提前将它们合并。

float rhoL = length(pos) * FOG_BASE_DENSITY;
float deltaY = abs(pos.y);

摄像机和片元的海拔可以像简单高度雾那样直接 cameraPosition.y 来求得，只需要再减去我们之前用来偏移浓度曲线的 FOG_BASE_DENSITY 就好：

float camAltitude = cameraPosition.y - FOG_START_HEIGHT;
float height = pos.y + camAltitude;

最后，取上我们的极限，如果在小于极限值则使用原函数：

bool limited = deltaY < 1e-12;

准备工作全部完成，可以来求了。先看原函数，拆成线性写法就是

翻译成 GLSL 之后就成了

const float f = FOG_BASE_DENSITY;
fogDensity = rhoL * exp(-f * altitude);

积分式也类似，线性写法是

翻译成 GLSL 就是

fogDensity = rhoL / (f * deltaY) 
           * abs(exp(-f * altitude) - exp(-f * camAltitude));

最后，我们使用雾气的负指数作为可见性

float visibility = exp(-fogDensity);

需要注意，我们现在混合的是场景可见性而不是雾气浓度，因此要记得交换 fogColorG 和 fragColor！

fragColor.rgb = mix(fogColorG, fragColor.rgb, visibility);

最终，我们完成了这个（或许不那么）艰巨的任务，让空间蒙上了一层神秘的面纱（你知道的，雾气这玩意就跟遮瑕粉一个道理）。由于我们使用指数积分，因此雾气的浓度与场景的视距进行了解耦，在大视距下由于天空的视口空间 Z 值会随之增大 ¹ ，天边的雾气也会随之变浓。此外，又因为我们使用了负指数的 Visibility，现在场景的遮蔽强度永远都不会超过 1 了。

[1] 天空总是会将 Z 值设置为远平面的值。如果视距仅为 2 区块，则区块边界的距离为 32，视口的远平面也就会被设置在这个距离附近。如果视距为 32 区块，则天边的区块边界的距离高达 512，天空就也被拉远了。

在进入下一章的体积光之前，一个让雾气看起来更鲜艳有层次的小技巧是根据光源方向权重来叠加使用天空颜色和雾色，比如：

float fogFactor = max(dot(lightDir, -viewportDir), 0.0);
vec3 fog = skyColorG + fogColorG * pow(fogFactor, 4);

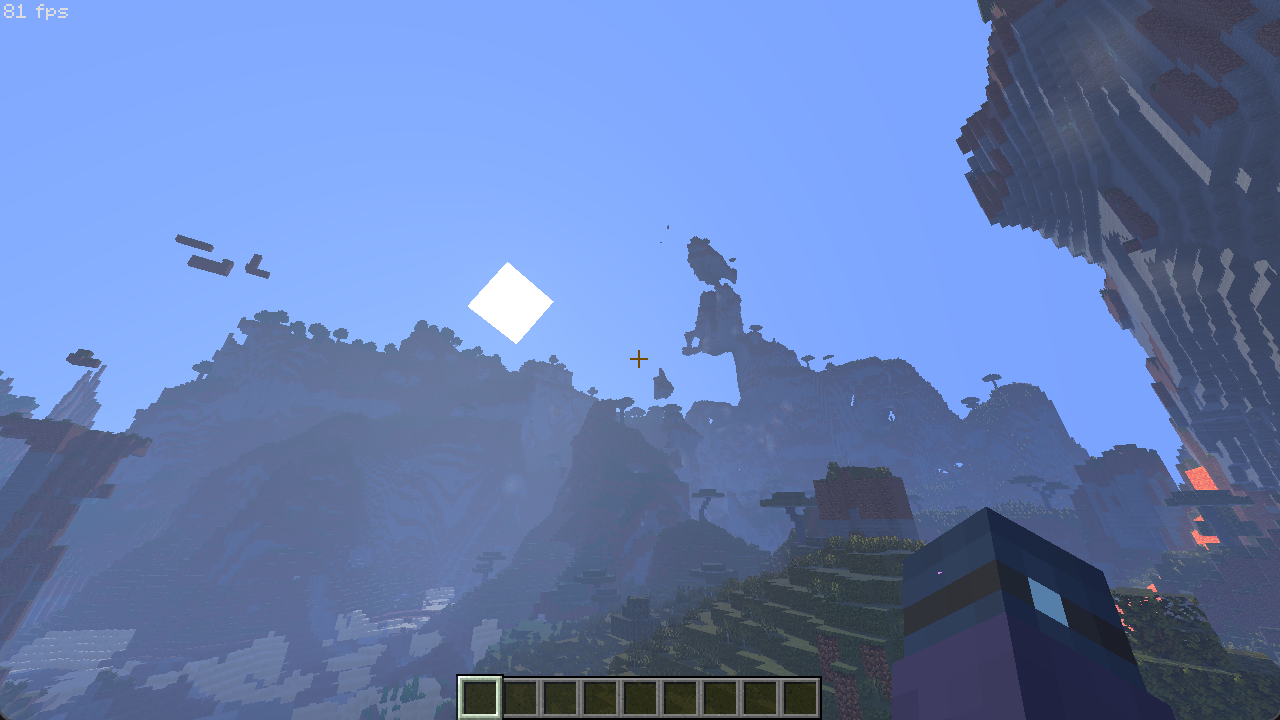
这些雾气性能逐级降低，因此你也可以视情况保留其他种类的雾气。

此外，也别忘了让雾色也影响环境光照：

float fogLumiFactor = max(dot(lightDir, surfaceNormal), 0.0);
// 环境光照相对来说可以更加平缓一些
vec3 ambientColor = skyColorG + fogColorG * pow(fogLumiFactor, 2);

float litSceneAmbient = [... 计算环境光照 ...];
litSceneAmbient *= AMBIENT_BRIGHTNESS * lightmap.t * albedo.a
                 * ambientColor;

简单大气

地球上有一层厚厚的大气保护着脆弱的生物圈，它不仅会散射强烈的宇宙射线，同时还会因为各种理化因素产生许多奇妙的效果。

我们之前已经完成了来自外太空的光照和贴近地表的雾气，然而目前它们仍然只是很机械地为地表提供恒定的光照和遮蔽。在这一小节中，我们会着手处理大气对它们的影响，并让纯色的天空更富活力。

日光、月光与环境

在第一章中，我们已经将场景的直接光照来源设置为了当前在场景中投影的太阳或月亮，然而，目前的光照颜色和亮度并不会随时间变化。在现实中，太阳光会被大气散射，从而在清晨和傍晚变得昏黄，而月光则是月亮反射来自太阳的光线，在晴朗的月圆午夜为地表提供微弱照明。

要想模拟大气光照就逃不开由瑞利散射（Rayleigh Scattering）和米氏散射（Mie Scattering）为基底构建的物理天空体系，但在进入物理渲染之前，我们不妨先利用一些俺寻思之力手动控制日光和月光的亮度与颜色。

正午日光色温约为 5000K (255, 231, 204)，在傍晚时则更接近 2000K (255, 141, 11)，在清晨，为了区别于日落，我们还可以将颜色设置得偏粉。虽然月光在现实世界中是暖色，但在艺术化作品中我们更倾向将它设置为 8000K (227, 233, 255) 的冷色（你也可以考虑到将傍晚和黎明的月光设置得更偏黄）。我们先将它们设置好：

const vec3 SunNoonColor = vec3(1.0, .91, .8);
const vec3 SunSetColor = vec3(1.0, .55, .04);
const vec3 SunRiseColor = vec3(1.0, .45, .31);
const vec3 moonColor = vec3(.89, .91, 1.0);

不同时间段的光照亮度也会不断变化，因此我们还需要更多有关世界时间的变量。还记得我们在第一章的某个小知识中介绍的有关时间的统一变量吗？

uniform int worldTime;
uniform float sunAngle;
uniform float shadowAngle;

在游戏规则 doDaylightCycle^{1.21.11 25w43a 及以前} 或 advance_time^{1.21.11 25w44a 及以后} 为 true 的世界中，时间刻 worldTime 每游戏刻增加 1，每个游戏日共 24000 时间刻，即现实世界 20 分钟。

表达太阳和投影源在天空中真·百分度（1.0 = 360°）的 sunAngle （）和 shadowAngle （）就基于世界时间， sunAngle 指示了太阳的位置，而 shadowAngle 则指示了目前投影源的位置。

从上个游戏日的第 23215 刻到第二个游戏日的 12785 刻，阴影空间原点在太阳位置，此时；
在 12786 刻时，太阳刚刚落到地平线以下，阴影空间原点切换到月亮位置，此时、；
12786 ~ 23214 刻，阴影空间原点处于月亮位置，此时；
同样，在第 23215 刻时，阴影空间原点切换到太阳位置，此时。

OptiFine 没有直接提供月光的角度，我们可以直接使用 moonAngle = fract(sunAngle + 0.5) 来求得， fract(x) 函数的内部实现为 x - floor(x) ，对于正数，它可以返回小数部分。

有了颜色和时间，我们就可以通过插值来在指定的时间段混合出指定的颜色了。太阳和月亮在游戏中说到底还是两个不相关的光源，因此，我们会将它们的颜色进行拆分。此外，为了让光照的亮度与颜色解耦，我们还会额外单独处理两组亮度参数：

vec3 sunColor;
float sunBrightness;
float moonBrightness;

根据经验估计，日落持续时间约为，而日出则是，这里的 1.1 即是次日。

我们依旧使用 smoothstep(a,b,x) 来处理它们，还记得它的用法吧，将在上平滑地映射到。对于日落来说很简单：

float sunSetRatio = smoothstep(.4, .5, sunAngle);

而对于日出来说，由于其跨越了一天， sunAngle 会归零，因此我们需要在归零的两段都进行额外插值然后相加：

float sunRiseRatioDay1 = smoothstep(.9, 1.2, sunAngle);
float sunRiseRatioDay2 = smoothstep(-.1, .2, sunAngle);
float sunRiseRatio = sunRiseRatioDay1 + sunRiseRatioDay2;

你会发现我们并没有完全按照日出和日落的规律设置光照颜色，这是因为在日出前半段和日落后半段，太阳沉入天边，场景无法受到阳光照射，下面设置光照强度时我们也会考虑到这一点。

由于在时会为 1，进而在时导致，因此我们需要在时归零：

float sunRiseFactor = float(sunAngle <= .2);
float sunRiseRatioDay1 = [...];
float sunRiseRatioDay2 = [...];
sunRiseRatioDay2 *= sunRiseFactor;
float sunRiseRatio = [...];

然后就到了我们的超绝穷举时间：

bool isSunRise = sunAngle >= .9 || sunAngle <= .2;
bool isSunSet = sunAngle >= .4 && sunAngle <= .5;
sunColor = isSunRise ? mix(SunRiseColor, SunNoonColor, sunRiseRatio)
         : isSunSet ? mix(SunNoonColor, SunSetColor, sunSetRatio)
         : SunNoonColor;

我们不关心日落之后的时间，因为那时日光已经不再影响场景色彩了，因此我们将日出和日落之外的时间全部设置为了正午的颜色。

亮度也可以使用类似的方法，因为亮度是周期性变化的，因此我们可以使用 smoothstep() 配合加减法来随时间调整亮度：

sunBrightness = smoothstep(0.0, .1, sunAngle)
              - smoothstep(.45, .48, sunAngle);
sunBrightness *= SUN_BRIGHTNESS;

你或许注意到了，我们将插值时间点偏移了一些，这是为了模拟在日月交替的时候亮度骤降的效果，所谓黎明前最黑暗的时刻，并且还可以用来作为阴影空间突变的缓冲和遮瑕。这也是之前我们将光照颜色变化集中在日照区间的原因之一。

类似的，月光亮度也可以使用这样的方法进行处理：

[... Settings ...]
#define MOON_BRIGHTNESS 0.2
[... final.fsh ...]
moonBrightness = smoothstep(.52, .6, sunAngle)
               - smoothstep(.85, .97, sunAngle);
moonBrightness *= MOON_BRIGHTNESS;

最后，我们将亮度和颜色乘入之前的直接光照公式中：

float litScene = [... 计算直接光照 ...];
litScene *= sunBrightness * sunColor
          + moonBrightness * moonColor;

为了让环境光照在日月交替这段至暗时刻中不那么突兀，我们也可以将日月光照作为额外系数乘入环境光强度中：

litSceneAmbient *= sunBrightness + moonBrightness;

现在场景中的光照强度终于会随着时间的变化而变化了！

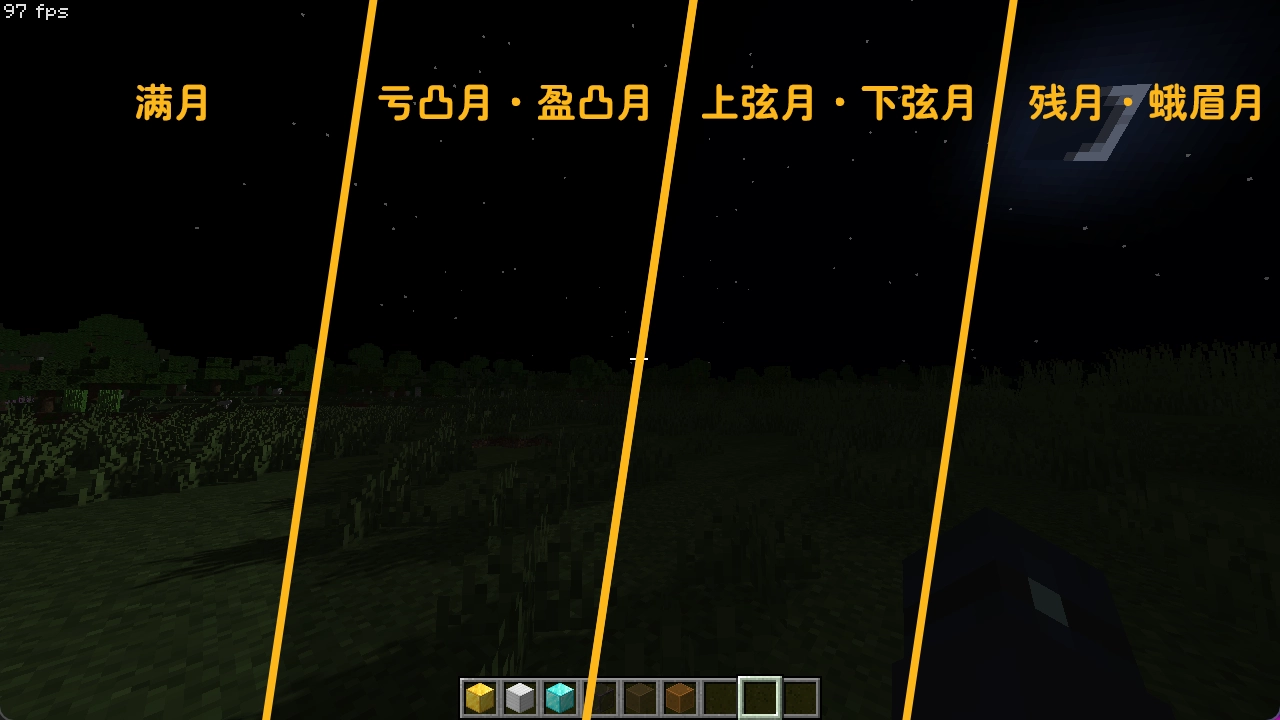
月相

除了时间之外，Minecraft 还存在月相，当太阳被地球阻挡而无法照亮月球时，月球产生的漫反射理应减少，来自月亮的“直接”光照就会减弱。月相与世界日挂钩，从第一天的满月开始到第八天的盈凸月为一个周期。Optifine 为我们提供了月相变量：

uniform int moonPhase;

它的值域为，在第五天月相为新月时， moonPhase == 4 ，其余时间月相的对应光照亮度以新月为中心对称，我们可以据此计算得到月相的亮度级别 abs(moonPhase - 4)。

当场景为满月时， $亮度级别月相$ ，如果将满月时的光照系数视为 1，则可根据亮度级别求得光照系数：

float moonPhaseLuminance = float(abs(moonPhase - 4)) / 4.0;

最后，将月相亮度乘入月光即可：

moonBrightness *= moonPhaseLuminance;

天气

除了日月循环，天气对光照的影响也不容忽视。在 Minecraft 中存在三种天气：晴天、雨天和雷暴。而雨天和雷暴视群系而定，又会出现降雨、降雪和阴天三种情况。

在本小节中，我们主要着重于光照的变化，其他效果，例如水坑和雨雪等会在今后的章节逐步添加。OptiFine 只提供了晴雨的转换，因此我们只能将雷暴按照雨天处理。

当天气由晴转雨时，天空颜色会转为灰色，光照变得柔和，让场景的观感饱和度也慢慢降低，此外，露天表面的反射率也会增加。为此，我们需要获取当前的降雨强度和“湿度”：

uniform float rainStrength;
uniform float wetness;

rainStrength 表征了当前降雨的强度，而 wetness 则可以用于表征地表的“湿度”。 wetness 由湿润半衰期和干燥半衰期控制：

const float wetnessHalflife = 600.0f;
const float drynessHalflife = 200.0f;

湿润半衰期控制由湿转干时的值跌落至起始值一半的游戏刻，默认为 600 刻，干燥半衰期则控制由干转湿，默认 200 刻。晴转雨时空气的湿度会迅速上升，而雨转晴后湿度降低会相对较慢，因此我们就沿用默认的设置了。

画面右侧显示了降雨强度和湿度在湿润半衰期为 5、干燥半衰期为 1 下晴雨切换时的值变化情况。可以看到降雨强度变化与天空色和雾色的变化直接同步。

被云层遮挡的光照

让我们从光照开始。当降雨强度增大时，由于太阳被云层遮挡，光照会减弱，再加上云层的向内散射，阴影也会由于“光源”的扩散而逐渐模糊 ¹ 。因此，我们可以在直接光照和阴影的 PCF 半径上动手脚。

[1] 太阳附近的云层会透射更多的太阳光，从而形成一个大范围的柔和间接光源。

雨天的直接光照完全消失不太好看，也会让模糊的阴影失去意义，因此我们保留 0.1 倍左右的光照强度。光照强度与降雨强度为负相关，我们需要手动映射它们。在此推荐一个类似 remap() 的线性映射函数：

#define remap2(a,b,c,d,x) ((x-a)/(b-a)*(d-c)+c)

它可以将从线性映射到上，或者说函数图像是一条过和两点的直线。

它的配套规整函数

#define remap2Saturate(a,b,c,d,x) clamp(remap2(a,b,c,d,x), min(c,d), max(c,d))

可以将映射后的值限制在上。映射是无序的，因此可以与成对交换，即

我们希望在降雨强度为 0 时光照强度为 1，降雨强度为 1 时光照强度为 0.1，因此我们需要将它们的关系映射到过和点的直线上，我们将两点代入 remap2Saturate() 中，就可以求得光照强度：

[... Settings ...]
#define RAIN_BRIGHTNESS 0.1
[... final.glsl ...]
float litScene = [... 计算直接光照 ...];
litScene *= sunBrightness * sunColor
          + moonBrightness * moonColor;
float rainFactor = remap2Saturate(0.0, 1.0,
                                  1.0, RAIN_BRIGHTNESS, rainStrength);
litScene *= rainFactor;

对于阴影的模糊，我们可以仿效光照强度，将 PCF 的半径倍率作为一个与降雨强度相关的系数：

[... Settings ...]
#define PCF_RAIN_FACTOR 5.0
[... Lighting ...]
float calcPCF(...) {
    [...];
    for(...) for(...) {
        vec2 steps = [...];
        steps *= remap2Saturate(0.0, 1.0,
                                1.0, PCF_RAIN_FACTOR, rainStrength);
    }
}

在低亮度下，大半径小采样的 PCF 带来的亮度断层不明显，也不会产生太多穿帮。现在，雨天的光照和阴影看起来也非常不错了：

被雨水打湿的材质

雨水落到物体表面后可以分为两种情况：在表面滞留或者被材料吸收。在本小节，我们暂时不考虑不规则的低洼地带导致的水坑效果，而是考虑当它们均匀地覆盖在表面或被吸收的效果。

在处理滞留和吸收的水之前，我们需要考虑哪些表面会在雨天被打湿。不难思索，只要是朝上且上方不存在的表面，或多或少都会沾到雨水。对于方向，我们可以使用视口空间法线与 OptiFine 提供的视口空间天顶坐标

uniform vec3 upPosition;

做点积，即 float up = dot(surfaceNormal, normalize(upPosition)) 。或者，我们还可以使用世界空间法线与做点积，我们知道法线的模长总是为 1，而点积是将两向量的对应分量相乘相加，因此我们只需要世界空间法线的分量即可。要想求得世界空间法线，一种办法是使用模型视口空间的逆矩阵：

uniform mat4 gbufferModelViewInverse;
[... main ...]
vec3 worldNormal = (gbufferModelViewInverse
                    * vec4(surfaceNormal, 0.0)).xyz;

然而求得完整的世界空间法线非常不划算，需要一次 float4x4 * float4 或者 float3x3 * float3 ，我们只需要世界空间法线的分量。来看看的元素如何排列：

逆矩阵左上角的块意义与原矩阵类似，每一列表示视口空间中的一个轴在世界空间中的朝向，而每一行则表示视口空间中每个轴的朝向在世界空间一个轴上的投影量。

要想求得世界空间法线的分量，我们需要将视口空间的法线全部投影到世界空间的轴上，也就是说我们只需要计算第二行的前三个分量，即：

float up = gbufferModelViewInverse[0].y * surfaceNormal.x
         + gbufferModelViewInverse[1].y * surfaceNormal.y
         + gbufferModelViewInverse[2].y * surfaceNormal.z;

只需要两次乘加和一次乘法就搞定，开销与 dot(surfaceNormal, normalize(upPosition)) 相比还少了一次 normalize()。

求得了表面方向，我们接着来判定表面是否被遮挡。就目前来讲，我们是无法准确地知道表面的上方是否有物体遮挡的，因为每个顶点甚至都无法访问临近顶点的数据，更别说其他的方块了。不过我们确实有办法间接估计，还记得天空光照吗，Minecraft 使用 Flood Fill 算法从上至下蔓延天空光照，当路径上有散射光照的方块时，天空光照就需要从临近的竖列蔓延过来，从而导致光照等级减一，越大型的天花板下，天空光照就会越弱。这给我们提供了一个思路：使用天空光照等级来判断光照被遮挡的情况。

之前，我们将天空光照压缩到了，游戏中的天空光照一共 16 个等级，也就是，雨水不会完全竖直落下，我们可以使用最明亮的两个光照等级来进行过渡，也就是 14 ~ 15，对应到 lightmap.t 就是 0.933 ~ 1：

float openair = smoothstep(0.933, 1.0, lightmap.t);

将这两个参数相乘，我们就能得到表面对雨水的“暴露”程度：

float exposed = saturate(up) * openair;

当然，这种估计方法对玻璃这类不会散射天空光照的方块就无能为力了。无论如何，我们终于可以开始处理表面被打湿的效果了，不妨从不透水材料开始。

水是无色的透明液体，因此当材料表面聚成水膜时，最简单的办法就是额外计算一层菲涅尔，反射部分取水体的反射，而折射部分则取附着材料的出射光照 ¹ 。据此，我们额外计算一套水膜的光照，注意，水膜只有反射部分，因此没有菲涅尔的光照（方块光照和基本亮度）不必计算：

[... Lighting ...]
// 水体的菲涅尔无颜色分量差异，你也可以直接使用 f_schilck 的同名重构函数。
float f_schilck_mono(float f0, float cosTheta) {
    return mix(pow(1.0 - cosTheta, 5.0), 1.0, f0);
}
float f_schilck_mono(float f0, float cosTheta, float roughness) {
    return f0 + (max(1.0 - roughness, f0) - f0)
                * pow(1.0 - cosTheta, 5.0);
}

[... final.fsh ...]
// 表面只需要计算基本的菲涅尔即可
vec3 litScene = calcLighting(...);
vec3 litSceneAmbient = calcLighting(...);

float wet_smoothness = wetness * exposed;
float wet_roughness = pow(1.0 - wet_smoothness, 2.0);
const float water_f0 = 0.02;

float fresnelWet = f_schilck_mono(water_f0, ndv);
float fresnelWetR = f_schilck_mono(water_f0, ndv, wet_roughness);
// 表面没有打湿时，菲涅尔强度降至 0
fresnelWet *= wet_smoothness;
fresnelWetR *= wet_smoothness;

vec3 litWet = calcLighting(vec3(fresnelWet),
                           litScene, // 使用附着材料的出射光作为折射部分
                           getSpecular(surfaceNormal,
                                       halfwayVec,
                                       wet_smoothness))
            * (sunBrightness * sunColor + moonBrightness * moonColor)
            * (lit * rainFactor);
vec3 litWetAmbient = calcLighting(vec3(fresnelWetR),
                                  litSceneAmbient,
                                  1.0)
                   * ambientColor
                   * (  lightmap.t
                      * AMBIENT_BRIGHTNESS
                      * (sunBrightness + moonBrightness)
                      * albedo.a);
#ifdef TXAO
float txao = [...];
litWetAmbient *= txao;
#endif
fragColor.rgb = litWet        // 将场景光照替换为水膜光照！
              + litWetAmbient // 环境光照也要记得替换！
              + litSceneBlock
              + litSceneBase;

[1] 也许你意识到了水膜反射掉的光线不再会照亮附着材料，因此表面会轻微变暗，需要在入射方向也计算一次水膜菲涅尔来求得水膜折射到材料表面的实际光照强度，但这种影响微乎其微，只有当入射光角度大时才会稍显差异，然而这时候主导表面光强的是光照的角度而不是水膜的反射，因而为入射再单独计算一次菲涅尔是不划算的。

当然，额外计算一次光照是很昂贵的，因此我们可以仅在雨天的裸露表面处理它们：

vec3 litScene = calcLighting(...);
vec3 litSceneAmbient = calcLighting(...);
vec3 litWet;
vec3 litWetAmbient;
float wet_smoothness = [...];

if(wet_smoothness > 0.0) {
    float wet_roughness = [...];
    float fresnelWet = [...];
    [...]
    litWet = calcLighting(...);
    litWetAmbient = calcLighting(...);
} else {
    litWet = litScene;
    litWetAmbient = litSceneAmbient;
}

litWet *= [...];
litWetAmbient *= [...];

庞大的计算量（目前来说还不算太大）让分支的开销变得可以接受，这样还可以直接忽略 up < 0 的情况。

接下来轮到透水表面了，透水表面意味着材料能够吸水，材料吸水之后由于光路变化，折射出的光线会减少，表面会显得暗淡。因此透水材料的表面处理就很简单了：

[... Settings ...]
#define POROSITY_DIFFUSE_DECAY 0.4
[... final.fsh ...]
litScene *= POROSITY_DIFFUSE_DECAY;
litSceneAmbient *= POROSITY_DIFFUSE_DECAY;

最后，我们来综合考虑这两种情况，如果你还记得 LabPBR 格式就再好不过了，高光纹理 Blue 通道中的表示了孔隙率！我们将其重映射到上就是：

int spec_blue = f2i8(material.b);
float porosity = remapSaturate(0.0, 64.0, float(spec_blue))
               * float(spec_blue <= 64); // 次表面散射材质的孔隙率始终为 0

孔隙率增大时，水膜的反射会减弱，表面的出射光也会变弱，因此我们可以改写之前的算法：

float wetLvl = wetness * exposed;
float diffuseDecay = remap2(0.0, 1.0,
                            1.0, POROSITY_DIFFUSE_DECAY,
                            wetLvl * porosity);
vec3 diffuse = [...] * diffuseDecay;

float wet_smoothness = wetLvl * (1.0 - porosity);

把雨天的光照系数稍微调高一些，看起来还算不错！

动图左侧是水膜的光滑度 wet_smoothness ，右下角的柱状图和之前一样，分别是降雨强度 rainStrength 和湿度 wetness。

当然，双层材质对我们目前这样简单的光照模型来说还是太大材小用了，你也可以尝试使用更加简单的最大反射来处理它。习题 4

本小节的雨天处理就到此告一段落，你也能明显地看出，这远不是雨天效果的完全体，等之后的章节中我们完成了反射后，画面的质量还会得到飞跃。

响应群系的大气

大气会因为当地气候的不同而呈现不同的样貌，Minecraft 的群系（Biome）也隐含了当地的气候，当我们移动到不同的群系时，大气的相关参数就会发生变化。

天顶与星空

改写环境光照

高动态范围

色彩映射

简单自动曝光

习题

尝试将简单高度雾的竖直方向改写为线性衰减的积分形式。我们需要进行分段积分：
- 如果片元和摄像机均位于，直接使用 remap(320.0, 63.0, altitude) 的积分式；
- 如果片元和摄像机均位于，则使用常量积分；
- 如果片元和摄像机有一个位于：
  - 若另一个位于，则使用，和在两个坐标之间选择；
  - 若另一个位于，则使用；
- 若片元和摄像机均位于则没有雾气。
最后，将它们乘入片元距离，再像简单水平雾那样进行幂次处理即可。
（主观题）在雾小节的末尾，我们用 lightDir 为光源附近的雾气进行了染色，然而效果并不太好，因为日月交替时 lightDir 会产生突变。为此，请仿效简单大气小节的内容，使用 sunPosition 和 moonPosition 求得独立的 sunDir 和 moonDir ，然后用它们配合 sunAngle 来进行光照过渡。你可以只使用雾色来叠加日光或月光颜色，而不是像之前那样还使用天空颜色。
（选做）使用 sunDir 和 moonDir 将直接光照拆成两个光源，然后将日光和月光的色彩、亮度和方向分别应用到两次光照上，形成平滑切换。记得在 sunAngle == 0.5 时将阴影从日光切换到月光上。
为雨水额外计算一次光照是很不划算的，特别是对目前我们这种简单的光照模型来说，可以使用一种更加精简的模型。
- 尝试将天气小节的水膜 F₀ 与表面 F₀ 取最大值并根据水膜光滑度混合，然后取表面和水膜光滑度的最大值用于反射和菲涅尔，只在直接光照和环境光照各执行一次 calcLighting()。
- 可以设置一个开关来在两种模型之间切换，双层材质在 PBR 中会有更好的效果。

09 二月 2026