延迟渲染中的光照 · 初识几何缓冲
空间与坐标系
在几何缓冲中,我们会将传入几何的顶点按照一定的方法进行坐标变换,这也是顶点着色器的核心部分。本节的内容较为复杂,但是要想编写好的着色器程序,理解空间变换的几何意义至关重要,因此请认真阅读。
局部坐标
GL 传入的顶点总是从局部坐标(Local Coordinate)开始。它代表了每批几何在以其自身为原点(具体原点取决于建模和生成时)的空间中所处的位置,这个空间称为局部空间 (Local Space)。
世界坐标
将每一批几何都放置在特定的位置,从而让几何与几何之间、几何与场景之间形成相对关系,这就形成了世界坐标(World Coordinate)。它代表了每个几何相对所有几何构成的空间中所处的位置,称为世界空间 (World Space)。它可以通过局部坐标左乘模型矩阵 (Model Matrix)得到。
视口坐标(眼坐标)
以我们观察的视角为原点,将所有几何按照特定角度位移和旋转,从而将场景移动到我们的眼前,这就形成了视口坐标(Viewport Coordinate),也被称为眼坐标(Eye Coordinate)。它代表了每个几何相对观察点所处的位置,以观察点建系,这个空间称为观察空间 (View Space)。它可以由世界坐标左乘观察矩阵 (View Matrix)得到。
投影坐标
在计算机中,若想将三维场景映射到二维的显示屏上,我们需要进行投影 (Projecting),即将三维场景的特定区域按照特定方向投射到屏幕上,其称为投影坐标 (Projection Coordinate)。投影坐标定义了我们场景的可视范围,包含在边界之内的场景最终都将显示在我们的屏幕上 1 ,尽管它们之间可能互相遮挡。当投影完成后,所有处于边界之外的几何都将被裁切 2 ,因此这个空间被称为裁切空间 (Clip Space)。它可以由视口坐标左乘投影矩阵 (Projection Matrix)得到。
[1] 著名律师 成步堂 曾经说过:“ 要将思维逆转过来! ”。不是“边界限制了我们能看见的场景”,而是“在投影区域内就算不进行裁切我们也根本看不见边界之外的场景”。
[2] 见下节 标准化(归一化)设备坐标。
回想一下现实生活中,透过一个固定的画框(就像窗口或者门之类的)向外看,你会发现什么?画框里侧越远(越深),能看到的景物也就越多,也即近大远小。这是因为我们是从一个点(眼睛)观察场景,同样大小的物体所占的角度会随着远离观察点而减小。
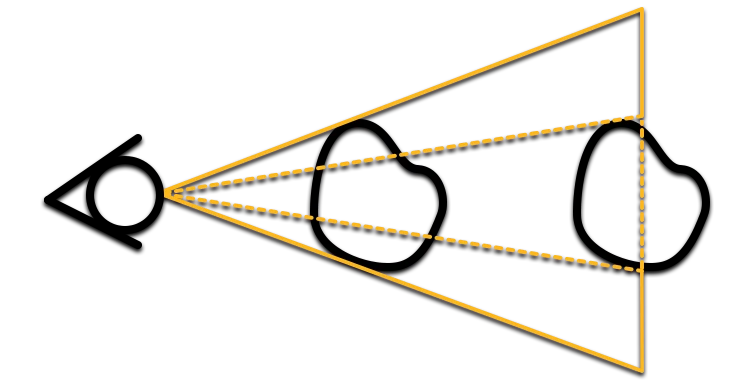
这种现象被称为场景透视 ,以这种方式进行的投影被称为透视投影 ,形成的像被称为透视视图 。与之相对的,严格按照坐标测绘,不产生近大远小的投影方式被称为正射投影 ,形成的像被称为等轴视图。
我们之前所说的投影坐标都基于正射投影,如果我们想要绘制透视场景,相较于一个立方体,我们需要一个平截头体作为边界。其推导在数学上比较复杂,在此不做讨论,你只需要记住最后至关重要的一步: 透视除法。
在第一节中你可能会好奇,我们明明是在一个三维空间中计算场景,为什么 gl_Position 却是一个四维向量。实际上,它的
由于 GL 使用的右手坐标系 3 ,视口空间的
[3] 举起你的右手张开,让手掌面向自己,你的大拇指指向的右方是
[4]
进行投影变换后,场景仍处于一个
标准化(归一化)设备坐标
事实上,透视除法还有另一个作用。还记得 GL 对标准坐标的执念吗?它希望场景中的所有的坐标最后都落在
在投影变换之后
觉没觉得有些熟悉?还没想起来?如果我们将它改写成
熟悉了吧?这正是第一节中我们将深度图深度转化到线性深度的公式!你可以使用 反函数计算器 自行尝试:
于是场景就从
其他两分量在裁切空间中的边界范围也与所在位置的
能够进入画面的几何数量由窗口的高宽或者说视场角(Field Of View)决定,Minecraft 使用竖直固定 FOV,这意味着 FOV 越大、窗口越宽,平截头体的尾部相较头部更宽,进入 NDC(或者说在裁切空间中小于
当转换到标准化设备坐标之后,GL 会执行栅格化 ,丢弃不可见的片元,然后将 gl_FragCoord 进行如下设置:
分量设置为以窗口左下角为原点的坐标,也就是像素的索引(整数)坐标加上0.5; 分量设置为线性映射 1 到 上(为了方便使用)的几何 值; 分量设置为裁切空间的 分量的倒数 2。
[1] 使用
[2]
最后,GL 会比较片元着色器执行完毕之后每个片元坐标的
空间变换
要想在坐标之间进行变换,我们要用到矩阵乘法 。我们的坐标总是从局部空间开始,直到投影空间结束
然后交由 GL 自行完成透视除法
在 Minecraft 中,我们不使用单独的模型矩阵
OpenGL 为我们提供了在上述几个空间中转换坐标的各种矩阵:
除了这些固定阶段使用矩阵外, JE 1.17+ 的核心配置中,OptiFine 还为我们提供了像内建矩阵那样根据每个程序动态设置的矩阵:
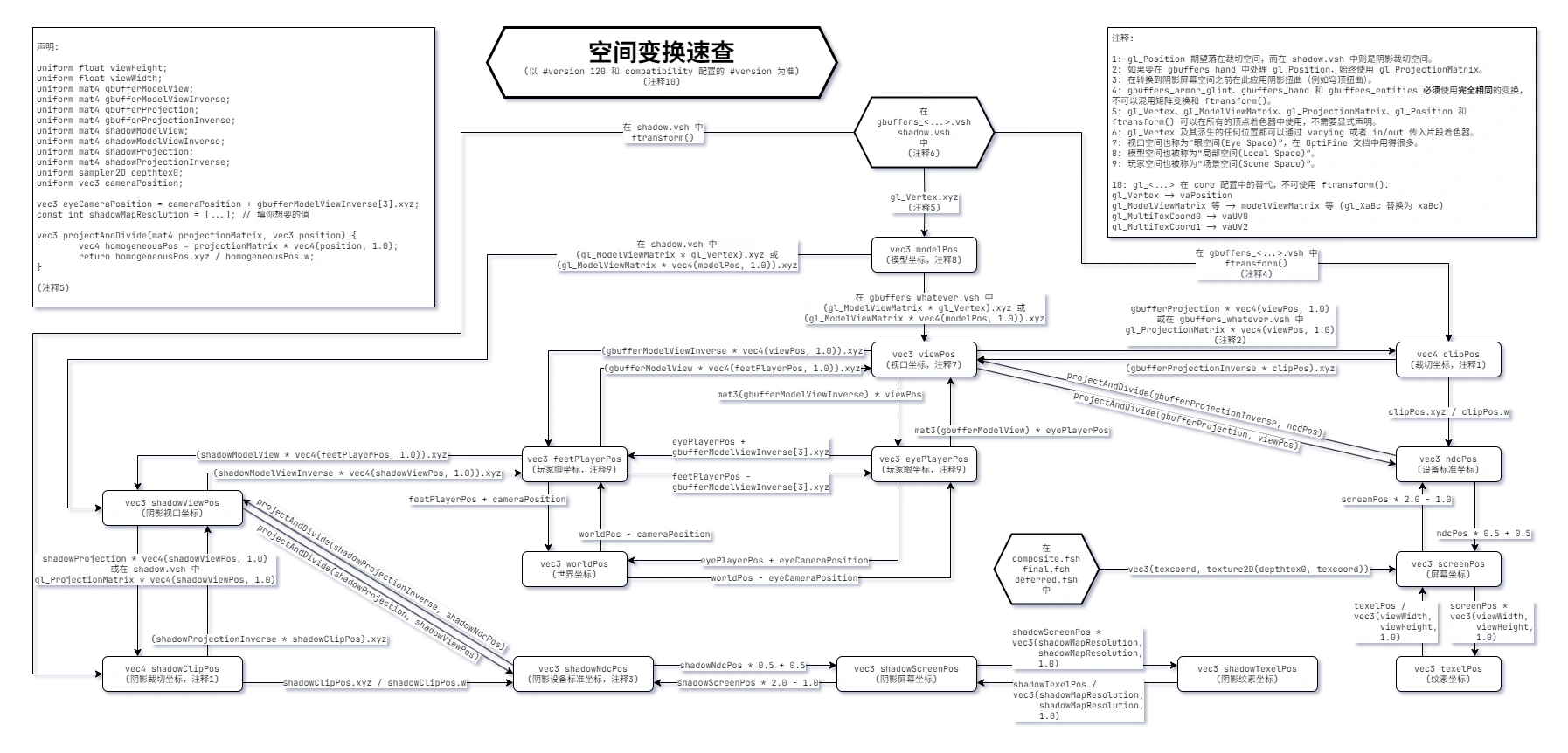
这张图整理出了各种空间之间的相互变换方法:
翻译自 shaderLABS Wiki ,你可以单击图片查看和保存附带深色背景的大图。该页面还提供了一个实时交互工具用于在每个空间中进行直观的变换。
几何缓冲
程序处理对象
还记得 结构和管线 中的几何缓冲管线吗?它们各自掌管一方,同时还要照顾自己那些擅离职守的下属管辖的几何。
gbuffers_basic负责无厚度线框和拴绳,无厚度线框包括调试区块边界,这个阶段没有纹理 ,只有顶点颜色。当该程序不存在时其所属几何交由内置管线处理。
gbuffers_line有厚度线框,包括方块选择框、碰撞箱、结构方块边框和渔线,这个阶段也没有纹理 ,只有顶点颜色。当该程序不存在时其所属几何交由
basic处理。gbuffers_skybasic负责天空中的无纹理内容,包括天空、地平线、星星和虚空,其中星星也由程序生成(实际上是由成对的小三角形拼成的方块),无需采样纹理。当该程序不存在时其所属几何交由
basic处理。gbuffers_textured负责大多数粒子。当该程序不存在时其所属几何交由
basic处理。gbuffers_skytextured负责太阳和月亮。当该程序不存在时其所属几何交由
textured处理。gbuffers_spidereyes负责原版实体发光,包括蜘蛛、幻翼、末影人和末影龙的眼睛。当该程序不存在时其所属几何交由
textured处理。gbuffers_beaconbeam负责信标光柱。当该程序不存在时其所属几何交由
textured处理。gbuffers_armor_glint负责盔甲附魔光效。当该程序不存在时其所属几何交由
textured处理。gbuffers_clouds负责原版云。当该程序不存在时其所属几何交由内置管线处理。
gbuffers_textured_lit负责发光粒子和世界边界。当该程序不存在时其所属几何交由
textured处理。gbuffers_entities负责大多数实体。当该程序不存在时其所属几何交由
textured_lit处理。gbuffers_entities_glowing负责发光实体的轮廓。当该程序不存在时其所属几何交由
entities处理。gbuffers_hand负责固体几何手持方块。当该程序不存在时其所属几何交由
textured_lit处理。gbuffers_hand_water负责半透明几何手持方块,如染色玻璃等。当该程序不存在时其所属几何交由
hand处理。gbuffers_weather负责雨雪粒子。当该程序不存在时其所属几何交由
textured_lit处理。gbuffers_terrain负责固体几何地形,世界中的绝大多数地形都由它接管。当该程序不存在时其所属几何交由
textured_lit处理。gbuffers_block负责方块实体,如箱子、告示牌和物品展示框等。当该程序不存在时其所属几何交由
terrain处理。gbuffers_damagedblock负责挖掘破坏效果。当该程序不存在时其所属几何交由
terrain处理。gbuffers_water负责半透明几何,如水和染色玻璃等。当该程序不存在时其所属几何交由
terrain处理。
第一个几何缓冲程序
我们的第一个几何缓冲将会围绕游戏中最为主要的世界地形(Terrain)展开,因为多数方块都属于这类,并且要素齐全(有顶点颜色、有实心和镂空纹理、受各种光照影响)。为了更集中精力地处理它,我们可以先将其他几何剔除掉。
回看上一节的内容,我们需要的几何大致都在 terrain 和 block 中,当几何缓冲着色器不存在时将会调用它们的父级着色器,于是我们只需要设法把 basic 程序设置为不输出内容,那么它下属的所有内容都会被清除。额外的,我们还需要单独将 water 和 clouds 清除,前者归属了 terrain ,而后者会在不存在时调用内置管线。
要想剔除一个着色器的片元内容很简单,只需要 discard 关键字即可,于是我们的 gbuffers_basic.fsh、 gbuffers_water.fsh 和 gbuffers_clouds.fsh 就可以临时写成
来剔除其他几何。
现在让我们从 gbuffers_terrain.vsh 开始吧。任何 GLSL 程序的第一步都一样:声明版本。接着, gl_Position 要求我们最终的坐标落在裁切空间中,然后交由 GL 进行透视除法。知道了这套标准程序,我们就可以实际上手将它们转写为 GLSL 代码了:
如果你跟着这样做并且重载了一番光影,你大概会得到这样一坨随着视角变化不断闪烁的东西:
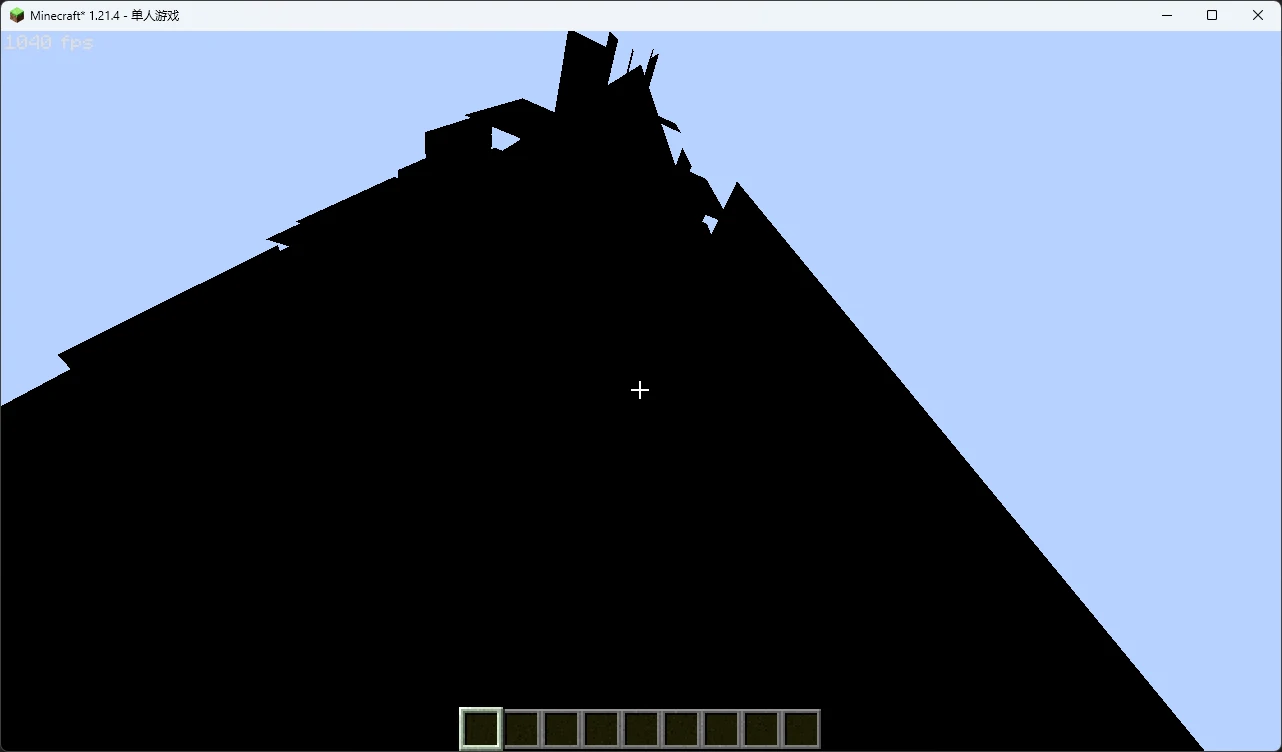
怎么回事?地形是逐区块绘制的,因此我们还需要知道每次渲染的区块的偏移坐标,当然 OptiFine 也确实提供了,我们只需要进行些许修改即可:
现在再次重载,你应该已经能从一团黑中看出一些轮廓了:
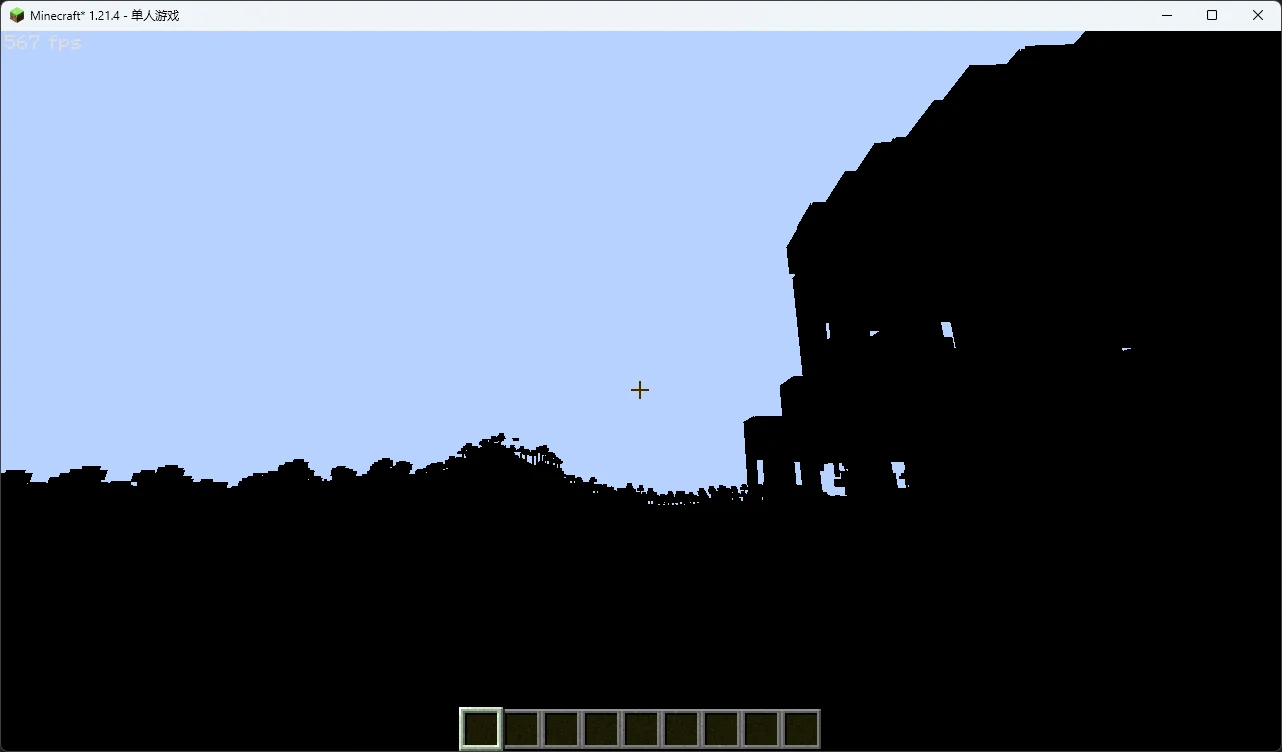
现在我们来编写片元着色器,让几何的颜色显示出来。OptiFine 为我们提供了顶点的颜色属性 vaColor ,我们可以直接将它传出
然后在片元着色器传入并输出
场景就初具雏形了:
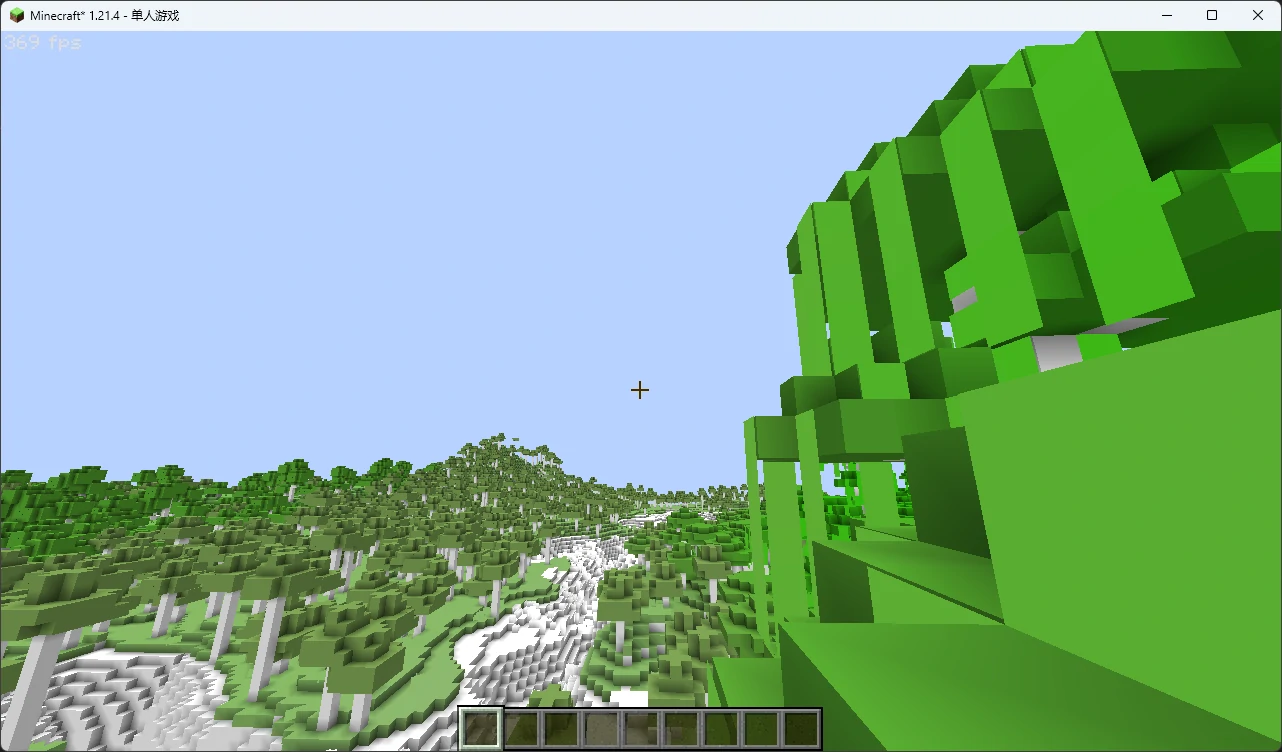
接下来,让我们为场景添加纹理。希望你还记得,首先我们需要在顶点着色器中获取顶点的 UV 。和延迟处理不同,几何缓冲的顶点纹理并不和屏幕坐标完全对齐,因此我们不能使用屏幕坐标来进行采样,只能使用 OptiFine 提供的 vaUV0。
此外,我们还需要一个纹理矩阵用于映射运动纹理(注意不是“动画”纹理,类似附魔光效这种平滑移动的就是运动纹理),尽管它在大部分着色器中都是一个单位矩阵,但是养成良好的初始化习惯极为重要。OptiFine 为我们提供的矩阵名为 textureMatrix:
几何缓冲中的颜色纹理名叫 gtexture ,在 terrain 中,它由所有方块贴图拼贴而成。我们只需要在片元着色器中声明它,然后像延迟处理那样采样即可:
然后你就会得到这样一个有些奇怪的场景,并且你会发现树叶的颜色不见了:
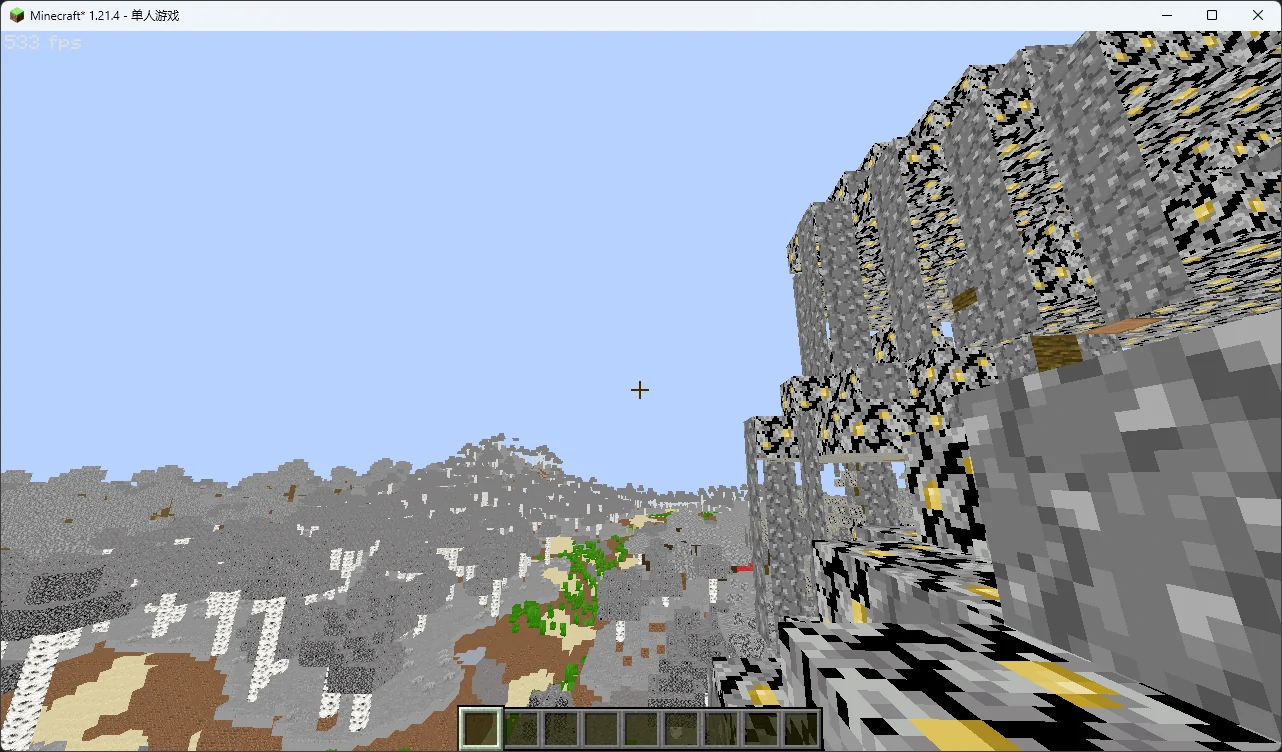
但是不要着急,还记得我们刚才传过来的 vColor 吗?它实际上是一个颜色乘数 ,我们只需要将它与纹理颜色相乘,魔法便出现了:
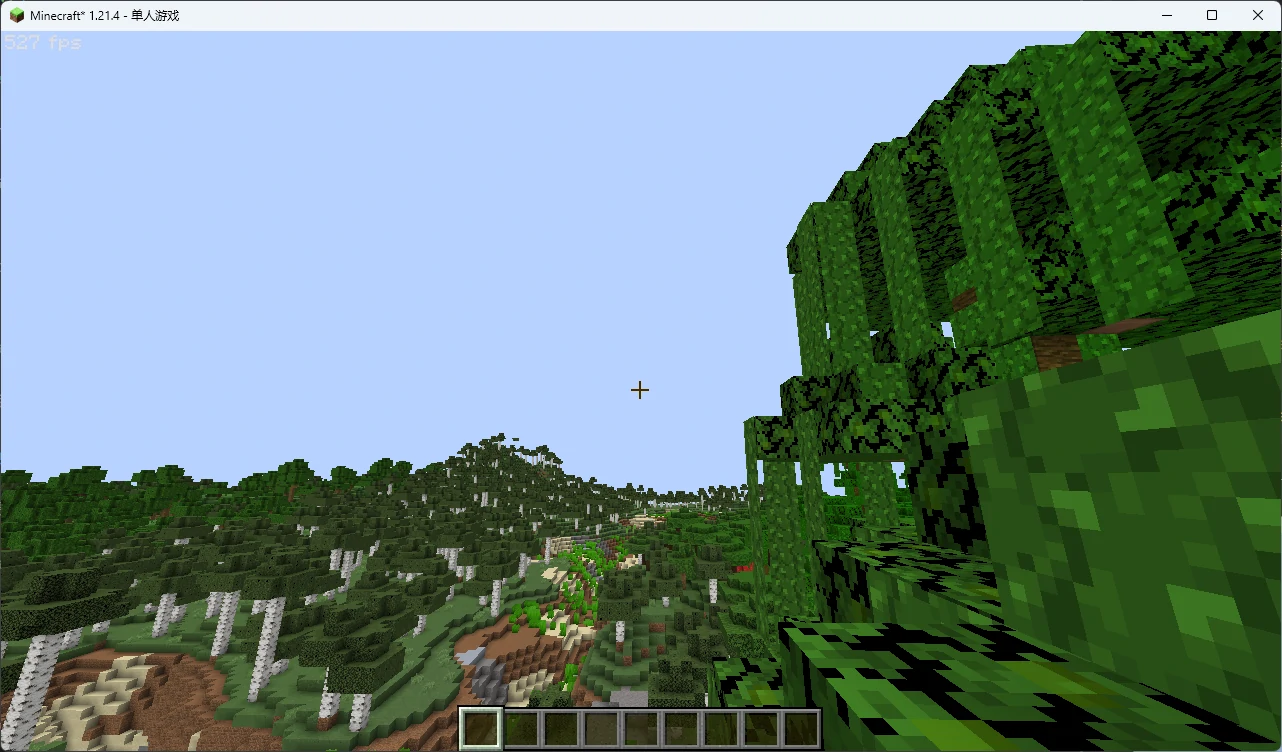
看起来有点内味了!除了某些不和谐的部分……我们的藤蔓怎么是不透明的呢?!这是因为固体地形默认不会进行色彩混合(我们将在之后认识它),也不会根据不透明度进行任何处理。还记得 结构和管线 (没错,又是这一节,基础很重要!)的约定吗?我们所在的 terrain 传入的均为固体几何 ,没有渲染半透明的必要。再结合之前我们提到的可以用 discard 丢弃片元,你应该已经有思路了:
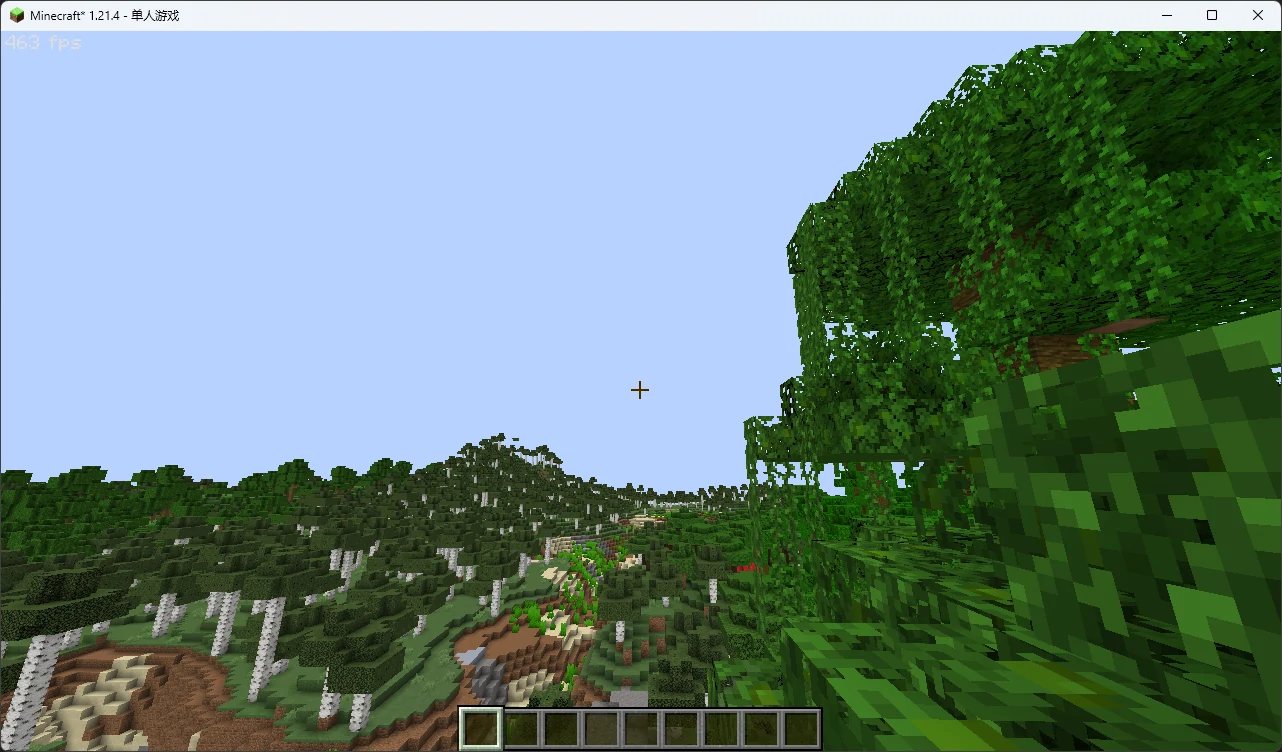
完美!上面这种通过不透明度丢弃片元的操作也就是所谓的 Alpha 测试 (Alpha Test,你可能偶尔会在各种地方看到这个名词)。你会注意到水体完全透明了,这就是将其他几何完全丢弃的效果。
最后,不要忘记把这一节新增加的统一变量和顶点属性放入我们之前的文件夹中!
分离顶点环境光遮蔽 · 再探光影配置
如果你仔细看过画面的输出效果,可能会疑惑:看起来场景中已经有光照层次了啊?
这是因为原版默认会将固定管线光照(仅根据表面朝向变化的光照,不包括光照贴图)烘焙到顶点颜色上(你可以在上一节仅输出顶点颜色的场景中看出来),OptiFine 为我们提供了关闭选项,在其设置中被称为 经典光效 。虽然我们可以直接在光影界面将经典光效改为 关 ,但是我们不能保证其他人也会知道需要这样做。要想强制使用不含光照的顶点色彩,仅输出场景颜色,也就是所谓的反照率 (Albedo) 1 ,我们需要回到 shaders.properties 再进行一些调整。
[1] 严格来说,表面颜色(大多数纹理基于此绘制)与反照率存在区别,前者是在均匀白光下物体呈现的颜色;后者则是“ 反向照明”的能力(固定光通量下漫反射的强度)。因此表面颜色实际上是反射和漫反射的混合,而反照率则是单独的漫反射(因此反照率纹理都会比同位置的表面颜色纹理暗一些)。我们会在下一章中进一步了解反射和漫反射。
在光影配置中,我们除了可以像上一节那样自定义统一变量、调整设置屏幕外,还可以进行很多设置。要想禁用经典光效,我们只需要添加:
回到游戏重载光影,你就可以发现方块侧面的明暗变化已经消失了。
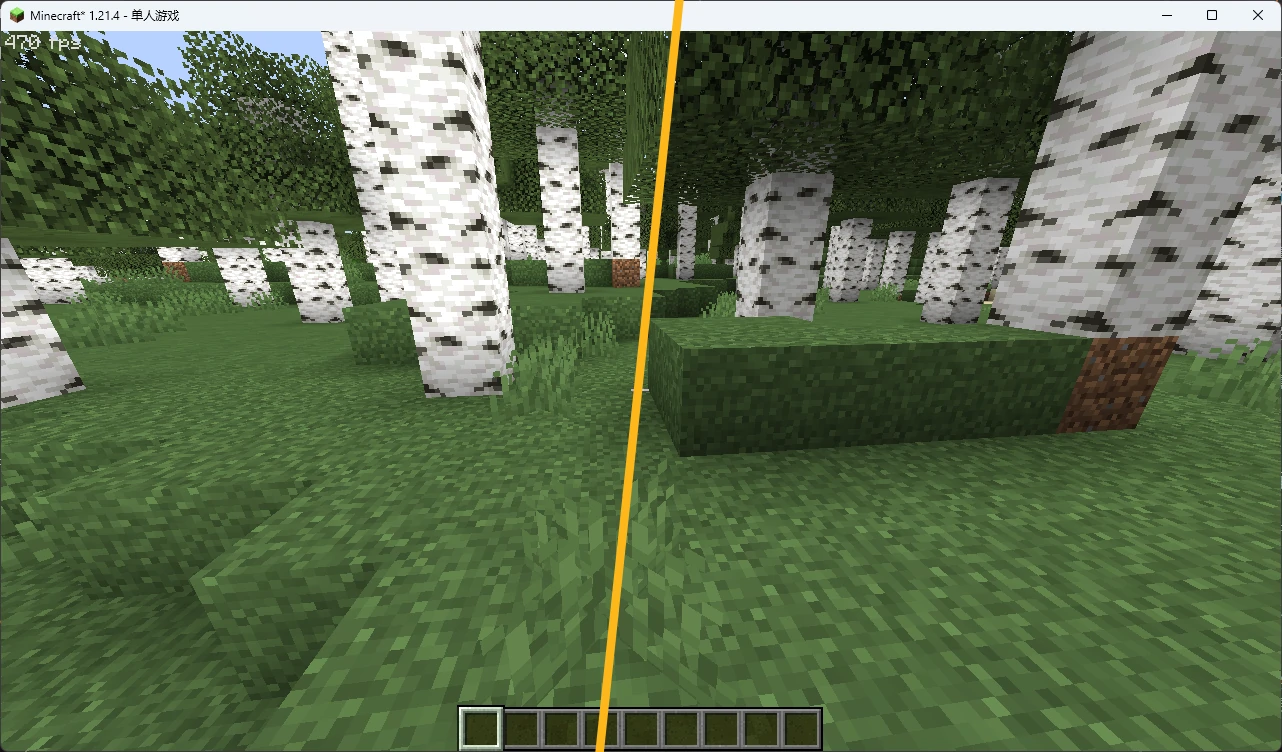
但是你同时也会注意到,方块接触处的阴影仍然存在,这是因为平滑光照会在接触区域添加 顶点环境光遮蔽 (Vertex AO)。但如果只是调整 平滑光照级别 也会面临和经典光效一样的问题。幸运的是,OptiFine 还为我们提供了分离它们的选项:
这个设置会将平滑光照所产生的顶点环境光遮蔽写入 Alpha 通道,这正是我们所需要的。
现在,我们就获得了场景的反照率了:
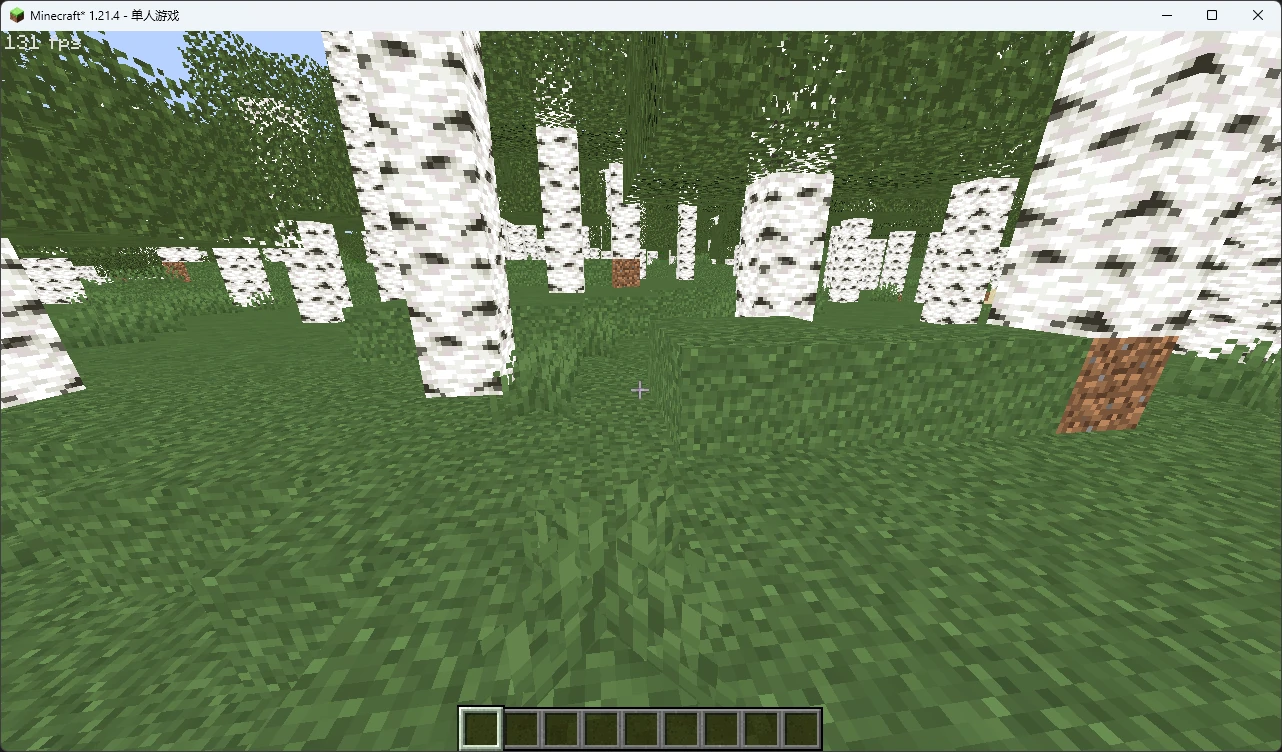
如果你好奇 AO 还能不能被正常渲染,可以在之前的 final.fsh 中尝试
然后你就会发现,AO 回来了,它们被妥善保存在 Alpha 通道中。但是如果你望向远处,会发现场景莫名变暗了:
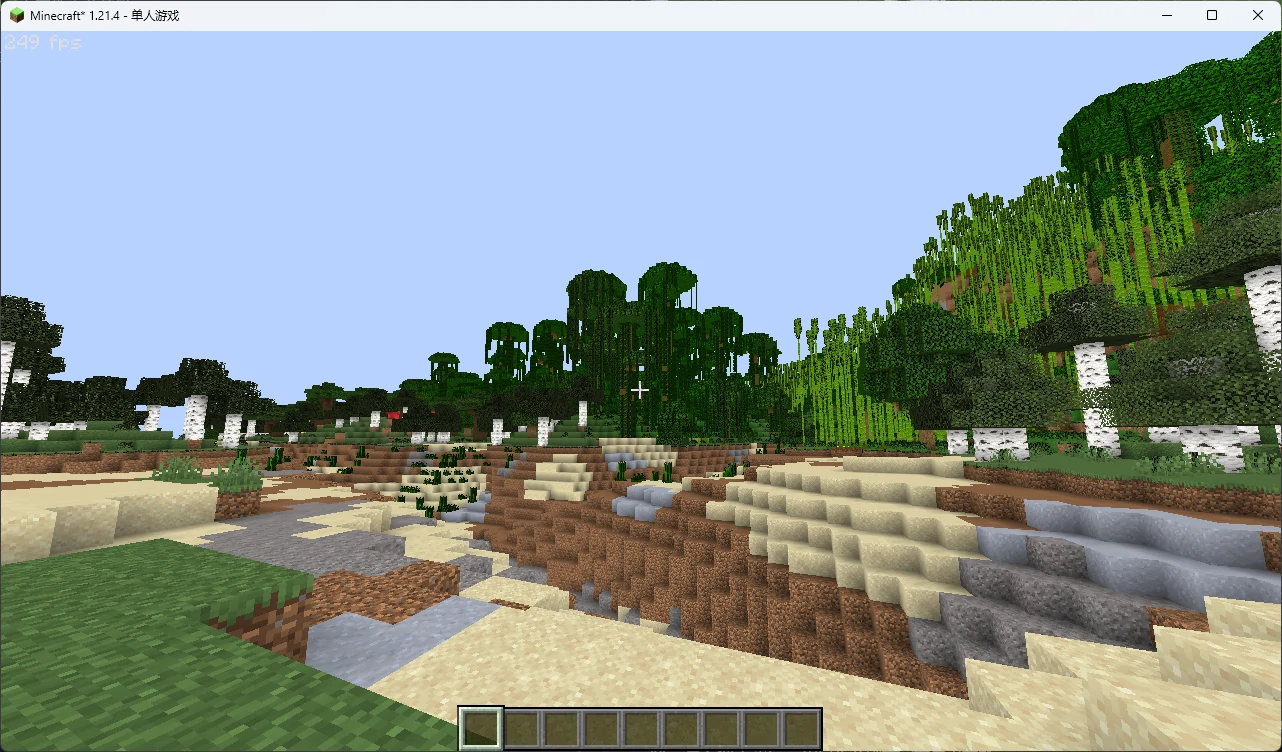
这是因为 OptiFine 默认开启了多级渐近纹理(MipMap),远处纹理的颜色,包括 Alpha 通道都由于降采样而将不透明(Alpha = 255)和完全透明(Alpha = 0)的像素混合成了半透明像素。
你当然可以直接把 MipMap 调成 关 ,但是还是那个问题:你没法控制其他玩家的行为。这个问题也很好解决,由于我们不需要半透明数据,因此可以在采样纹理之后立即进行 Alpha 测试,然后将最终数据的 Alpha 通道直接更改为 AO 数据:
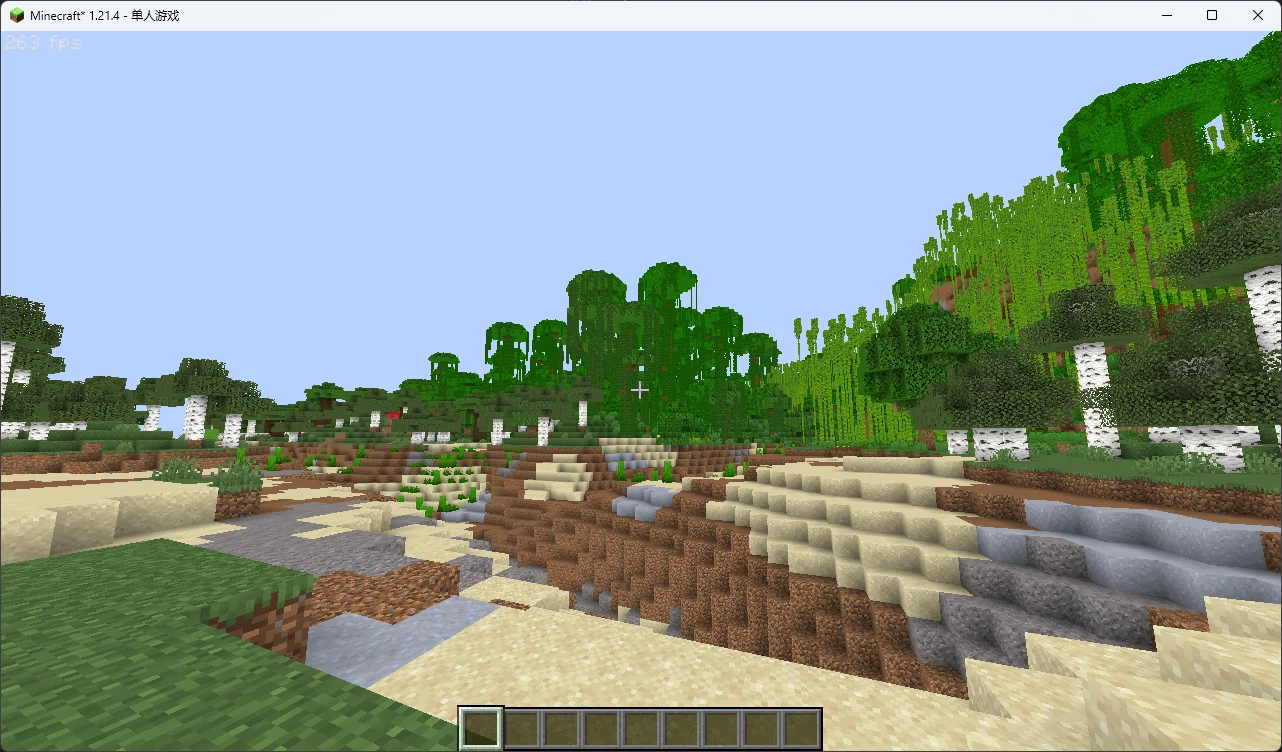
这样就正确了。
还原经典光照
希望你还没被上面的一大坨几何变换搞晕,因为接下来,我们就要进入重头戏了。要想还原经典光照,我们首先需要知道原版的光照方向和处理方法。
原版实现
由于原版地形直接将固定管线的光照烘焙进了顶点颜色(间接导致 OptiFine 的经典光效),而且无法直接找到光照方向的有关数据,要想完美实现原版光照,我们需要动用一些 俺寻思之力。
访问我们的 versions 文件夹,将游戏的 .jar 本体使用压缩软件打开
然后找到压缩包内的 \assets\minecraft\shaders\ 文件夹
将它们提取到 \resourcepacks\<测试包名称>\assets\minecraft\ 。记得在 \resourcepacks\<你的包名称>\ 下新建一个 pack.mcmeta 文件,然后在里面写上包数据以便游戏读取
然后在资源包中将其装载。
接着,我们使用 VS Code 将这个文件夹作为工作区打开,你可以在 \include\light.glsl 中找到 Mojang 用来处理光照的函数:
按下 CtrlShiftF 呼出工作区搜索这个函数,发现它主要在实体渲染中使用。我们可以点开渲染大多数实体的 entity.vsh ,可以看到向函数中传入的 lightDir0 和 lightDir1 是统一变量 Light0_Direction 和 Light1_Direction。
如果你直接去搜索这两个统一变量,会发现所有声明它们的 .json 文件都将其设置为了
即三个标量浮点组合,也就是 vec3(0.0) ,但是光照方向应该是模长为 1 的向量。这是因为它们实际上并没有被设置值,只是进行了默认初始化,在着色器使用它们之前会由游戏程序为其赋值。
我必须得吐槽一下 Mojang 居然还在用顶点光照……不过对于四四方方的 Minecraft 原版来说似乎也确实足够了。
这下麻烦大了,我们可不想大动干戈地去反编译游戏。但是别忘了:我们还可以修改着色器啊!接下来就来见识我们的惊世智慧吧。
回到我们的 entity.vsh ,思考一下,我们只需要找到它们的朝向就好,于是就又轮到我们的点乘函数 dot() 出场了。你可能还记得,它接受两个同维向量,并输出这两个向量的点乘值,但其实它还可以改写成
这里的 Normal ,它是几何的法向量,也称法线,即与几何表面垂直向外的单位向量(如果你真的不知道法向量是什么的话……)。这正是我们所需要的!
现在我们就需要委屈一下我们的顶点颜色了,在程序的末端我们将其覆写为点乘数据:
然后来到它的同名片元着色器文件 entity.fsh ,可以看到它的输出变量是
那么我们也可以在程序末端直接覆写:
最后回到游戏,关闭 OptiFine 光影,按下 F3T 重载资源包
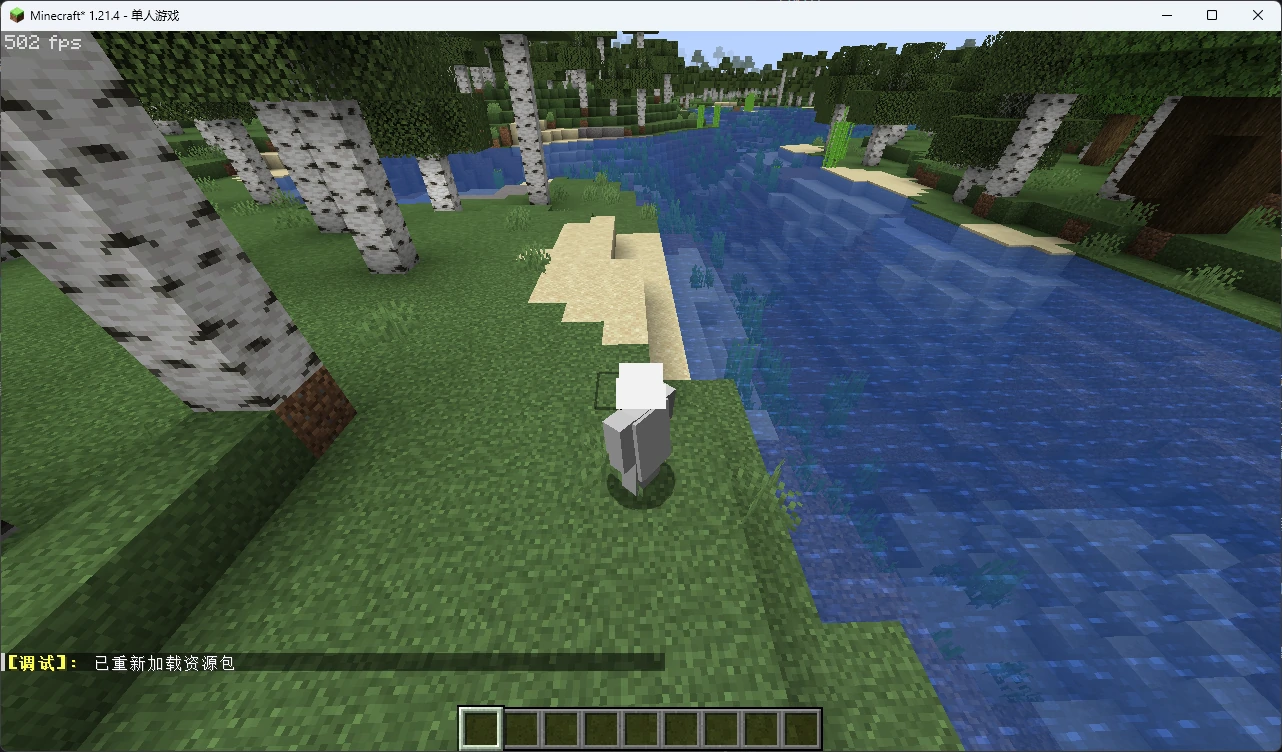
你就已经可以用自己的后脑勺(或者用第三人称正面模式,这样你就可以直接知道朝向)来找最亮的方向了。同理, Light1_Direction 也能这样找到。
最终你会发现, Light0_Direction 的方向是 Light1_Direction 则是
现在,让我们卸载掉测试资源包,回到我们的 OptiFine 光影,在 shaders.properties 中定义它们:
然后记得在 Uniforms.glsl 中声明它们
最后,把原版着色器定义的光照强度和光照函数也拷贝到 Settings.glsl 和 Utilities.glsl
编者习惯性地移除了前缀并改用驼峰命名,你也可以根据自己的习惯定义函数名。
法线与多缓冲区输出
如果你阅读了上一小节就会知道,要想在场景中实现光照,我们还需要几何体表面的朝向 ,即法向量或法线 。它是垂直于几何表面指向外侧的 单位向量 。OptiFine 当然为我们提供了它,我们直接声明对应的顶点属性即可:
和坐标一样,法线数据也需要经过空间变换。不同的是,变换法线数据时只需要改变它们的朝向,而且它们不应该受到透视投影的影响(还记得吗,透视投影在数学上是通过扭曲顶点位置实现的,因此也同时扭曲了表面朝向)。于是我们需要用到法线变换专用的法线矩阵 (Normal Matrix),在 OptiFine 中只需要声明:
就可以使用,它会将法线从局部空间变换到视口空间。最后在 gbuffers_terrain.vsh 中输出变换后的值就取到顶点法线了:
现在你可能会产生一些疑惑:就算我们把它传入了片元着色器,我们能传出的也只有 fragColor ,那法线数据怎么办?
这里就需要我们进行多缓冲区输出了。要想进行多缓冲区输出,最直接的办法是定义多个 out 值:
默认情况下 OptiFine 会根据声明顺序将它们放入对应索引的缓冲区,但是不要这样做 ,因为当输出缓冲区变多之后如果意外更改了声明顺序,或者想跳过缓冲区输出(比如只输出到 1 号和 3 号缓冲区),会导致很多不必要的麻烦。
一种办法是使用 layout 关键字自己指定要输出的缓冲区。我们可以使用 layout(location = X) 来指定输出目标:
这样,我们就指定了 fragColor 输出到 0 号缓冲区,而 normal 会输出到 1 号缓冲区,但这还仍然不够。
最标准的做法是使用 /* DRAWBUFFERS:ABC */ 和 /* RENDERTARGETS: A,B,C */ 来显式声明将要输出的缓冲区以及它们的索引顺序:
这两个指令的效果相同,但是前者缓冲区之间没有分隔符,因此只能指定 0 ~ 9 号缓冲区,而后者使用逗号作为分隔,可以指定所有缓冲区。
或
最后,我们在 gbuffers_terrain.fsh 中将它们输出到各自的缓冲区。需要注意的是,法线的分量范围是
有些未闭合的单面片(比如某些版本鲑鱼的尾巴和一些模组物品)可能会出现顶点法线方向反向的问题 1 ,因此我们需要将它们翻转回来。场景中的法线应该都是朝向视点所在的半球内的,另一半球朝向的几何都会被它的其他面遮挡,即法线与观察方向的夹角不会小于
[1] 因为只有一层顶点,法线数据只能有一个朝向,大多数面片模型比如矮草丛之类 Mojang 还是考虑到了的。此外,正常情况下游戏都会启用背面剔除,所以那些内外都可以看到纹理的几何实际上是两层不同的面组成的。
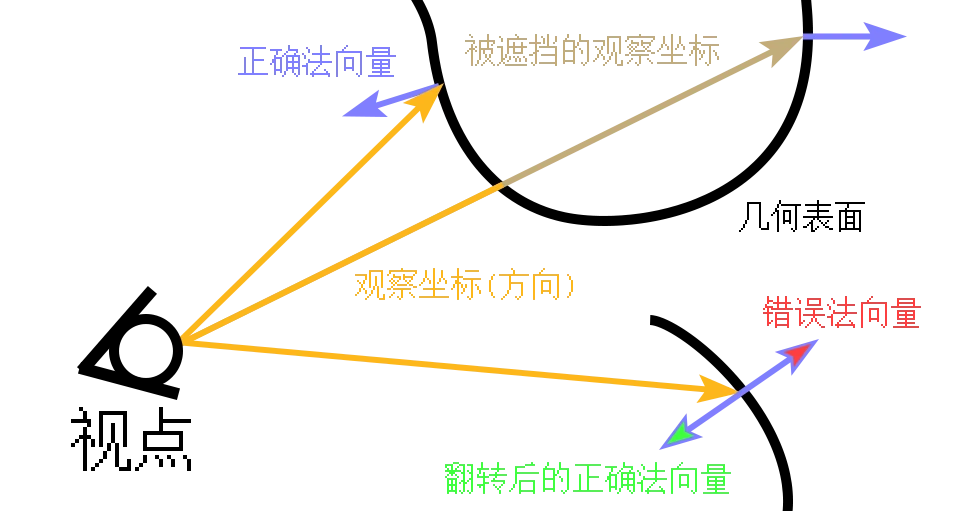
OpenGL 提供了判定当前片元是否为正面的内建变量,我们只需要在片元着色器中使用 gl_FrontFacing 即可判定:
回到 final.fsh ,如果你的操作正确,那么采样 colortex1 并直接输出的场景应该是这样:
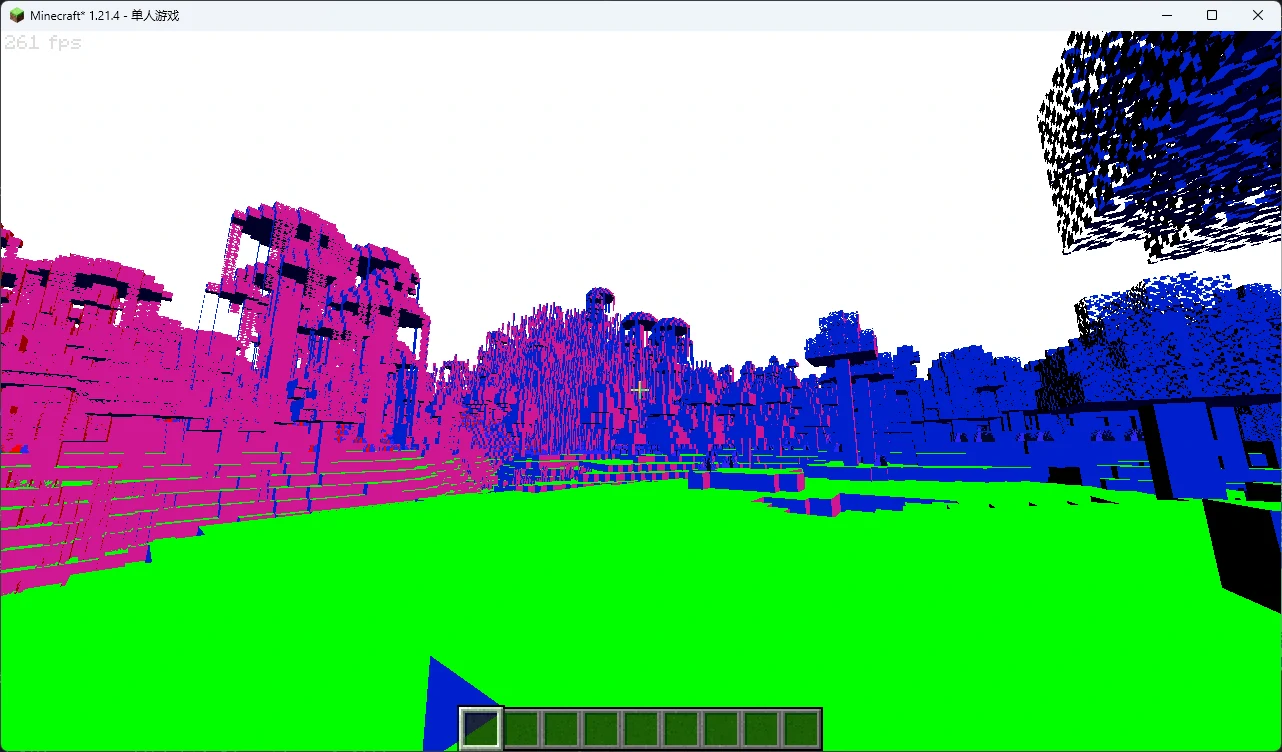
并且法线的颜色会随着视角的转动而变化。
至此,我们已经在几何缓冲中拿到了处理光照所需要的全部数据,接下来就可以进入延迟处理了。
在延迟处理中渲染光照
让我们直入主题,实际上手来利用之前获得的函数和统一变量处理光照。在处理任何效果之前,我们都应当先明确这些效果所处的空间。对于光照效果来说,只要所有信息都在同一正交空间中即可。由于我们的法线是视口空间,因此需要将光照方向也变换到视口空间:
所谓的光照方向就是指向光源位置的单位向量,我们使用 normalize(gvec vector) 函数就可以将任意非零向量转换为单位向量(其实我们在设置的时候就已经手动归一化 1 了)。你会注意到我们将光照向量的第四分量设置为了 0.0 而不是 1.0 ,这是因为 gbufferModelView 中包含了视角摇晃的位移数据
其中
[1] 这里的归一化和缓冲区、坐标系的归一化都有所区别,向量的归一化是将其转化为单位向量,缓冲区则是将每个通道都钳制到
[2] 这里的子矩阵与 附录 5 中的独立矩阵有所区别。此处的子矩阵仅表示矩阵块内特定的元素,附录 5 中的独立矩阵是合并应用矩阵的拆分形式。
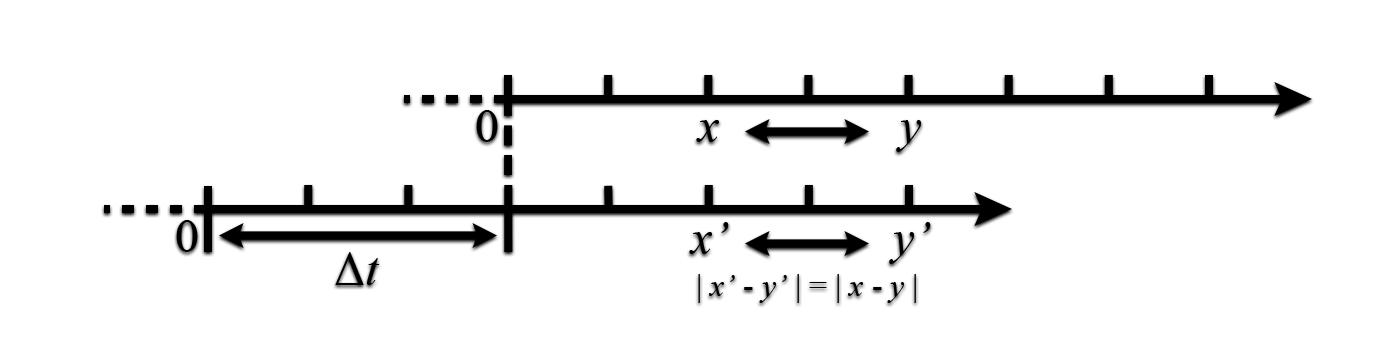
想象一下,当一个坐标系(世界空间)的一个坐标点转换到另一个坐标系(视口空间)下时,我们应该同时应用参考坐标系(摄像机)的位移,让点的位置随着坐标系(摄像机)的移动而变化;而当这个坐标是一个方向时,由于它只是一个固有的相对方向信息,与坐标系原点无关,就算我们的摄像机移动,它的朝向也不应该因此改变。
一个更简化的例子,假如我们在一维数轴上有一个点
数据类型 | 变换目的 | |
|---|---|---|
绝对位置(点) | 1.0 | 需要随相机位移和旋转才能获得正确的相对位置 |
相对位置(方向) | 0.0 | 只需要将其随摄像机旋转,其本身就代表了相对位置 |
当我们将向量乘入矩阵时,如果
而如果
有关矩阵乘法的细节这里不再过多展开,同时也感谢 Tahnass 对这一小节矩阵相关原理的解释!
然后将它们传入之前的函数中,就能看到,场景光照回来了!
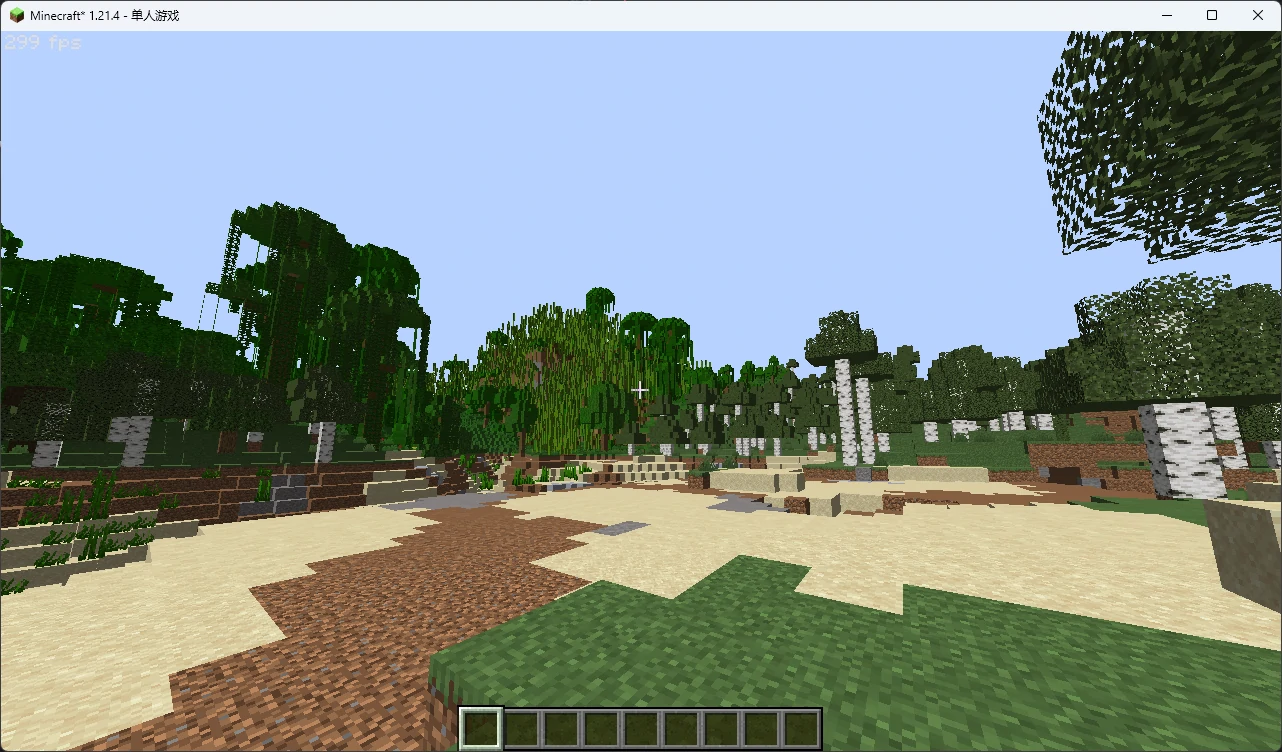
如果你还没忘记之前我们拆分进 Alpha 通道的 AO,记得把它也乘回来:
至此,我们在延迟渲染中还原的原版光照就完成了!
如果你抬头看天,会发现天空莫名变黑了,这是因为天空并没有写入法线数据,默认清除的白色与光照方向的点乘出现了问题。因此我们还要再次使用之前的 depthtex0 进行判定,当判定到天空(深度为最大值的 1.0)时使用原始颜色:
如果你将光影和原版对比,你会发现场景的明暗变化明显更强烈,这是因为我们使用的函数实际上用于实体光照,如果你想削弱明暗差距,可以调整之前拷过来的宏的值,把它们塞进设置屏幕也是一个不错的选择。
习题
尝试将法线信息转换到世界空间,记住我们在存储它们时的映射方式,以及区分法线到底是点还是方向。
尝试调整光照的分量从而改变方向,如果你不确定是否为单位向量,可以使用
normalize()函数归一化,但是要注意不要使用四维向量或者保持第四分量为0.0。