整理与规划

首先来看函数，当我们要在程序中调用函数时，必须在主函数之前声明或直接定义，为了程序方便，我们通常都直接定义。

在上一节，我们在 final 函数定义了四个纹理边界处理函数和两个边界判定函数。这几个函数算是比较常用的类型，如果今后我们需要在其他着色器中使用，最笨的办法就是把函数拷贝过去，不仅麻烦还容易出差错。再者，假如你拷贝完才发现，某个函数的实现出现了问题，这下好了，天塌了。而且随着程序的编写，函数肯定会越来越多，到时候我们想检查逻辑也会非常麻烦。

聪明的你肯定已经想了很久了：我们直接把这些函数塞进一个文件里，然后在着色器中使用 #include 调用它们就行。

这种文件就称为库文件 （或者说头文件），有了它可以极大提升代码可读性和易维护性。对于这类通用函数，我们都将它们存进一个名为 Utilities.glsl 的文件（意为实用函数），并将其后缀设置为关联到了语法插件的 .glsl。

tip

在原版资源包中，Mojang 添加了一个名为 #moj_import <namespace:file> 的宏用来包含库文件。和 OptiFine 的 #include 不同的是，它只能调用资源包任意命名空间中 shaders\include\ 文件夹下的对应文件。

如果你更细心一点，可能会觉察到另一个问题：如果我们重复包含一个文件会怎样？

这是可能的，因为有些库文件可能还包含了其他库文件，如果重复包含，编译器就会报告重复声明函数或变量而导致出错。这个问题也很好解决，还是我们的宏命令： #ifndef 。我们只需要在库文件的开头和结尾加上

#ifndef FILE_UTILITIES
#define FILE_UTILITIES
[...]
#endif

就可以完美避免重复包含的问题了：如果已经包含过这个文件，势必定义过 FILE_UTILITIES ，而如果已经定义了它，则直到对应的 #endif 之前的内容都不会被包含，也就跳过了整个库文件。

在上一节，我们使用了几个统一变量。如果你去看过 附录 1 就会知道，我们的统一变量和顶点属性之后肯定也会占个满屏。于是我们的第二个文件也准备好了： Uniforms.glsl ，它专门用来存统一变量。

有些统一变量（主要是纹理）并不是所有程序中都可用的，比如我们已经用过的 colortex0 就是一个仅延迟渲染可用的采样器。对于这类变量，我们可用主动在包含每个库之前进行声明来判断当前所处的着色器程序和阶段：

#define FINAL_SHADER
#define FRAGMENT_STAGE

然后在库文件中添加：

#if defined FINAL_SHADER || defined COMPOSITE_SHADER || defined DEFERRED_SHADER
uniform sampler2D colortex0;
#endif

如果你仔细阅读了 第一章第二节 就会知道 composite 和 deferred 是什么。

然后预留好几何缓冲专用的缓冲区判定宏：

#if defined GBUFFER_SHADER || defined SHADOW_SHADER
// 以后的几何缓冲专用统一变量都放在这里
#endif

tip

其实 colortex0 对应的缓冲区也可以在几何缓冲中访问，但是不能通过采样器访问，我们将在以后的章节提及。

由于只有顶点着色器才能访问顶点属性，我们将它们单独放入文件 Attributes.glsl ，然后只在顶点着色器中包含即可。

tip

如果你想了解所有 OptiFine 提供的统一变量和顶点属性，可以阅读 附录 1。

同样的，别忘记在两个库文件加上防止重复包含的宏：

Uniforms.glsl
 {...}

Attributes.glsl
 {...}

还记得我们之前因为懒得手改数据而定义的宏 BLUR_SAMPLES 吗？这些宏定义可以当作游戏内光影设置页面的选项。为了之后提供更加友好的用户选项界面，以及防止一些选项需要跨文件导致改动不及时，把它们存起来也是必要的。我们把它们都保存在 Settings.glsl 中以供调用，同时也不要忘记：

Settings.glsl
 {...}

如果把它们就这样散乱在 shaders 文件夹下，如果今后库文件增多会变得麻烦，我们可以在下面新建一个文件夹 libs ，然后把它们拖进去。

└─ shaders
   ├─ libs
   │  ├─ Attributes.glsl
   │  ├─ Settings.glsl
   │  ├─ Uniforms.glsl
   │  └─ Utilities.glsl
   └─ <着色器程序>

现在，我们把所有占地方的内容全部整理好了，现在我们只需要用 #include 包含它们就好。要记住 #include 的路径总是从 shaders 开始：

#include "/libs/Uniforms.glsl"
#include "/libs/Attributes.glsl" // 原始数据靠上放置，以确保其他文件能够调用
#include "/libs/Settings.glsl"
#include "/libs/Utilities.glsl" // 确保自定义内容在数据下方，以便能取到所有数据

不知道你还记不记得，在之前的程序中我们定义了两个变量：

vec2 screenSize = vec2(viewWidth, viewHeight);
vec2 pixelSize = 1.0 / screenSize;

它们本质上都是用统一变量运算而来的，统一变量在一个着色器的每个像素之间都不会更改（纹理只是可以更改采样位置，每个像素都能访问统一位置的数据，所以也是统一变量）。自然而然地，我们就会思考：能不能只计算一次这些统一变量呢？

这里需要光影包很重要的配置文件了，希望你还记得之前第一章的内容，在这里我们要用到配置文件就是 shaders.properties 。它使用类似初始化文件（.ini ）的语法，可以进行很多配置、调整光影选项页面、以及我们所需要的：添加自定义统一变量。

tip

你可能在思考是否能用 const 类型，这要求编译之后其内容完全不变，但我们能自由调整窗口尺寸。

定义自定义统一变量的语法非常简单：

uniform.vec2.screenSize = vec2(viewWidth, viewHeight)
uniform.vec2.pixelSize = vec2(1.0 / viewWidth, 1.0 / viewHeight)

注意不能像 GLSL 那样混用浮点和向量，也不能进行向量四则运算。

然后，我们可以像声明其他统一变量那样声明：

uniform vec2 screenSize;
uniform vec2 pixelSize;

记得把它们放进 Uniforms.glsl 中。

tip

自定义统一变量还有很多参数可以使用，具体可以查阅 自定义统一变量。

warning

在配置文件中使用 # 开头来编写注释可能导致 Iris 读取出错！

还记得我们孤零零躺在 Settings.glsl 里的宏吗？事实上，如果对它改造一番，我们就可以不需要每次都在代码里修改它的值了。试着在这一行后面加上注释，然后把几个值用方括号括起来，同时以空格隔开每个值：

#define BLUR_SAMPLES 5 // [3 5 7]

然后在配置文件中添加一行

screen = BLUR_SAMPLES

最后保存并回到游戏重载光影，按下 F3O 打开光影设置页面，如果不出意外，你应该已经可以看到它了：

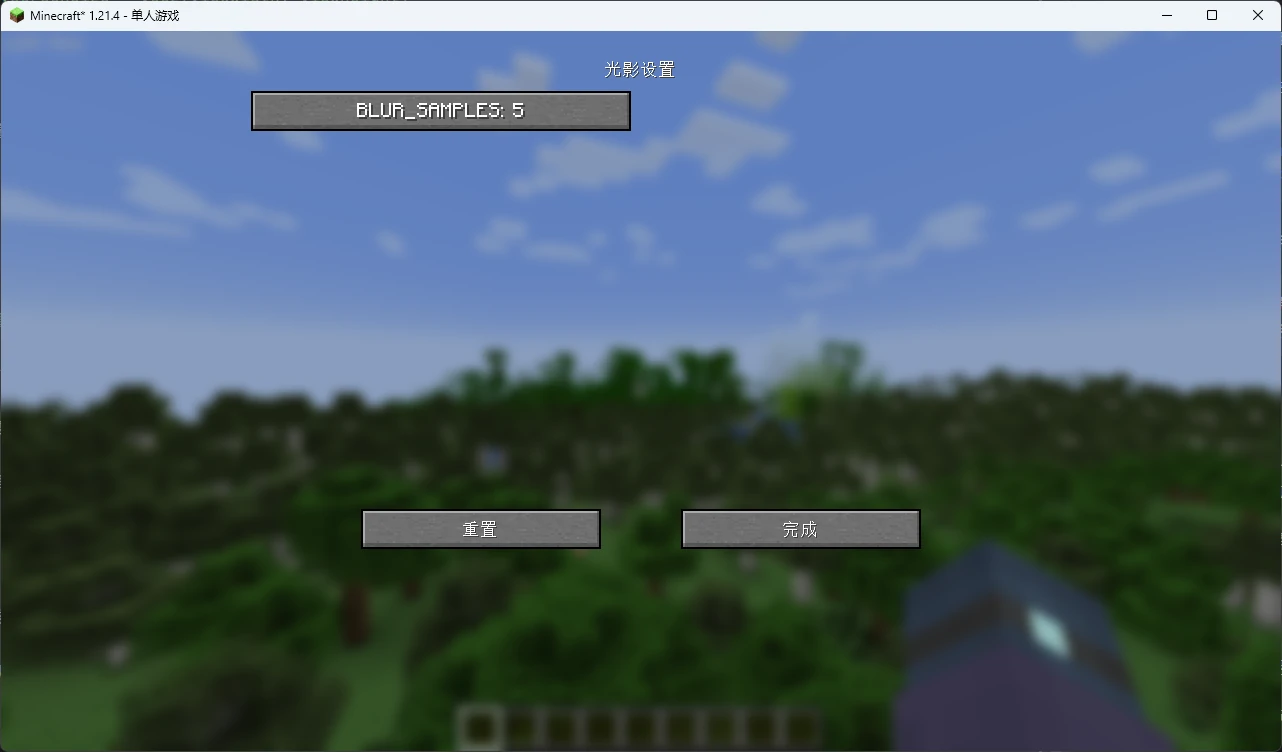
试着点几下这个选项，你会发现它在我们之前设定的几个值中来回循环，这就是我们的光影选项了。假如你再在配置文件中添加一行

sliders = BLUR_SAMPLES

然后保存并重载，你会发现选项变成了滑块：

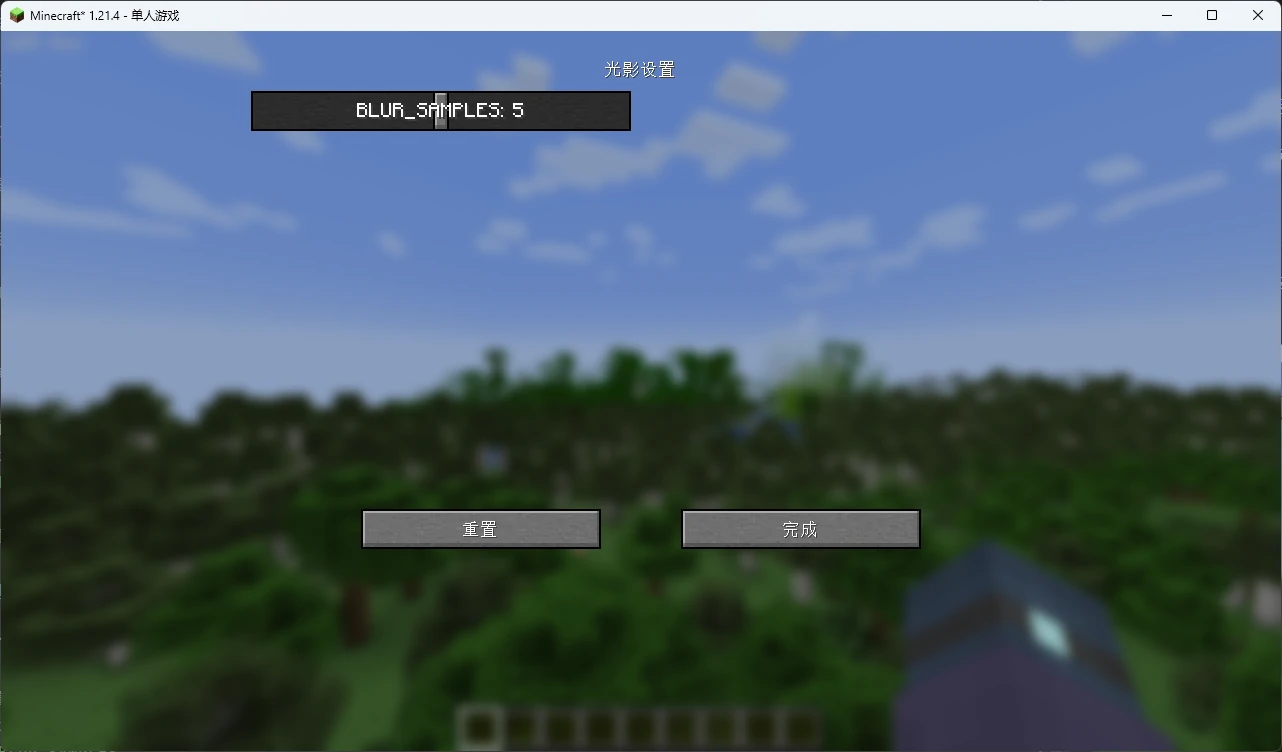
这对目前的我们来说已经够用了。在之后的章节中，我们将更具体地讲解光影选项。