实现：比率法线与转换

背景

1. 法线贴图通常由软件根据纹理自动生成。然而对于低分辨率纹理，软件生成并不理想，且我们期望能精确地调控；

2. 我们很难将手绘法线的三分量控制在理想范围内，但在某一分量上增减会导致另一分量变动，不同分量上的倾斜角度也不够直观；

3. 尽管 LabPBR 将 分量所在的 b 通道 另作他用 在一定程度上缓解了模长小于 的问题，但是当 时，用于重建 分量的算法 将产生非实根，从而导致 NaN 错误。

古人的智慧

SPBR 的开发者 Shulker 最初使用手算法线表 （一张向四周发散的法线图），在其上进行取色并绘制法线。

这样虽然可以避免法线不按预期工作，但是其仍存在以下弊端：

• 依赖数据表，不好预期倾斜角度，难以保证变化曲线（特别是除中心点四方向外的法线）；

• 角度受限（取决于数据表的分辨率）；

• 由于 b a 通道另作他用，在更改法线时只能使用下列两种方法：

  1. 在 r g 通道同一位置分别使用同一数据绘制；

  2. 将 b a 通道独立，然后覆盖绘制图片，最后再将 b a 通道回覆盖。

• 吸色太烦人了。

解决方案

我们拟采用一种新格式，设法在前期绘制时将 r g 分量较长的分量视为 、 轴向 轴倾斜的比率 ，两个分量的比值作为倾角，由此，若法半球在 内，则 时可以获得完美的 斜角。

当绘制完成之后，我们使用算法将其转换为标准法线（Standard Normals，简称 SN，角标使用 ）。

根据其按比率控制倾角的特性，我们将其命名为比率法线 （Ratio Normals，简称 RN，角标使用 ）。

推导

我们期望法线都在半径为 的法半球上，而比率法线的则在边长为 的正方形上，那么就需要将 映射到 。

虽然将二维映射到三维看起来有点不自量力，不过和 LabPBR 一样，我们使用 重建 分量，因此我们主要的任务是将 映射到 ，看起来就简单多了。

我们将 记为 ，并将范围限制在第一象限（使用 即可扩展到四象限），作从原点到 的线段并延长，与矩形边界的交点为 我们就获得了下面这张图：

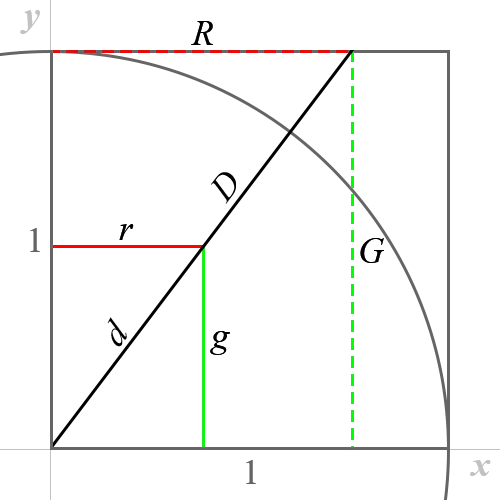
我们从图上可以知道， 与 的关系式为

然后，我们记对角线

其比值为

则以对角线为轴（记为 轴），与 轴成平面，并在 处作平行于 轴交于标准圆的直线。如下图：

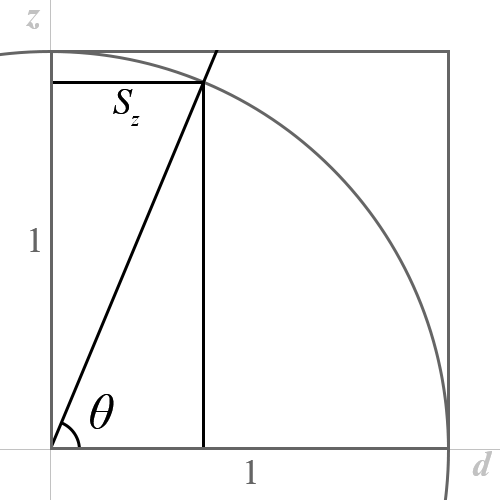
由于我们只能自由地控制 和 的值，于是期望在这个平面上的表达不要过于复杂

于是我们在该平面上使用反三角函数来求得其角度的比率。

于是

将其从 映射到 并作为 的放缩参数，记为

化简

我们从图 1 不难看出， 、 中必定有一个值或两个值等于 ，同时也隐含了等于 的边 对应的相似边 大于或等于另一边 的相似边 ，例如当 时， 。

当 时

同理，当 时

于是我们可以将 化简为

为了让其适配实际在 区间上的法线，我们需要对函数进行处理，于是最终的公式就变成了

这样一个简洁优雅的算法。

绘制比率法线

现在绘制就变得非常简单了，如 解决方案 所说， r g 通道较大的一个值现在会作为法线 分量与 平面的夹角比率，而 r g 通道值之间的比值则会作为在 平面上的倾角，由于后期需要重建，与几何表面垂直的比率法线应当是 r = 0.5, g = 0.5 ，就和普通法线一样。

比如当 r = 0.25, g = 0.6 时 分量与 平面的夹角就为 ， 平面上的角度则可以使用基本三角函数直接计算。

算法